用一次不等式或者一次方程式的形式來(lái)表示的幾個(gè)制約條件下,求一次式中目標(biāo)函數(shù)最大或最小的最優(yōu)值的方法o作為最優(yōu)化或作戰(zhàn)計(jì)劃(OperationsReserch,簡(jiǎn)稱O.R)的方法被運(yùn)用。
■求制約條件下的最大/最小值
線性規(guī)劃法就是在滿足成本AW1000日元的一次不等式或一次方程式所表示的制約條件下,求出使銷售額目標(biāo)函數(shù)最大化或最小化的變最(如銷售量、電話外呼次數(shù))的方法。
■曾被應(yīng)用于第二次世界大戰(zhàn)中
線性規(guī)劃法始于第二次世界大戰(zhàn)中美國(guó)、英國(guó)的作戰(zhàn)計(jì)劃。制定空中爆炸計(jì)劃后,如果多添加轟炸機(jī)的燃料就能擴(kuò)大行動(dòng)范圍,但是可以裝載的炸彈數(shù)目就不得不減少;相反地,炸彈數(shù)目越多,可以裝載的燃料就變少了。在這樣的制約下,為了達(dá)到最佳的作戰(zhàn)效果,計(jì)算燃料和炸彈的最佳裝載量就成了線性規(guī)劃法的起源。
■在高中數(shù)學(xué)里已經(jīng)學(xué)過(guò)
不喜歡公式的人大概對(duì)到此為止的解說(shuō)敬而遠(yuǎn)之,但其實(shí),簡(jiǎn)單的線性規(guī)劃問(wèn)題早已在高中數(shù)學(xué)中學(xué)過(guò)。不知道你對(duì)下頁(yè)圖還有印象嗎?
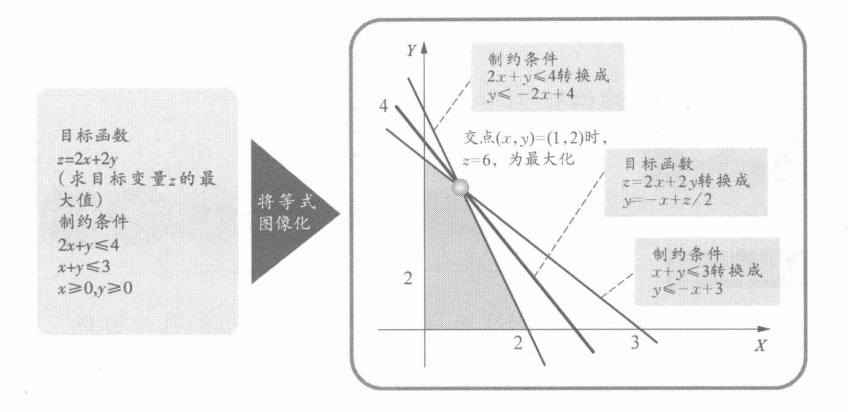
如上圖,先把制約條件的公式圖表化,在符合制約條件的灰色區(qū)域里,用相符合的坐標(biāo)值,代入目標(biāo)函數(shù),最后得到最大值和相應(yīng)坐標(biāo)。線性規(guī)劃法將之進(jìn)行了發(fā)展及應(yīng)用,增加了變量和制約條件,能解決目標(biāo)變量更為復(fù)雜的問(wèn)題。
■線性規(guī)劃法的應(yīng)用領(lǐng)域
線性規(guī)劃法是思考者本身可以算出數(shù)學(xué)最優(yōu)解的簡(jiǎn)便方法,在眾多領(lǐng)域中都有實(shí)際運(yùn)用。如:
•軍事、航天工業(yè)方面的軌道計(jì)算問(wèn)題
•制造相關(guān)的生產(chǎn)計(jì)劃問(wèn)題
•物流業(yè)相關(guān)的配送問(wèn)題
•醫(yī)藥業(yè)相關(guān)的配制問(wèn)題
•電話外呼業(yè)相關(guān)的清單計(jì)劃問(wèn)題