前言
本篇章主要介紹二叉樹的應用之一------二叉排序樹,包括二叉排序樹的定義、查找、插入、構造、刪除及查找效率分析。
1. 二叉排序樹的定義
二叉排序樹 ( B i n a r y (Binary (Binary S o r t Sort Sort T r e e , B S T ) Tree,BST) Tree,BST),也稱為二叉查找樹,具有以下性質:
(1) 若左子樹非空,則左子樹上所有結點的值均小于根結點的值;
(2) 若右子樹非空,則右子樹上所有結點的值均大于根結點的值;
(3) 左、右子樹也分別是一棵二叉排序樹。
綜上可知,在二叉排序樹中:左子樹結點的值 根結點的值 右子樹結點的值,所以對二叉排序樹進行中序遍歷,可以得到一個遞增的有序序列。
2. 二叉排序樹的查找
二叉排序樹的查找是從根結點開始,沿某個分支逐層向下比較的過程。若二叉排序樹非空,先將給定的關鍵字與根結點的關鍵字進行比較,若相等,則查找成功;若不相等,如果小于根結點的關鍵字,則在根結點的左子樹上查找,如果大于根結點的關鍵字,則在根結點的右子樹上查找。
二叉排序樹的查找算法:
def BSTSearch(self, k):
TreeNode = self.RootNode
while TreeNode is not None and k != TreeNode.data:
if k TreeNode.data:
TreeNode = TreeNode.lchild
else:
TreeNode = TreeNode.rchild
return TreeNode
3. 二叉排序樹的插入
二叉排序樹作為一種動態樹表,它的結構通常不是一次生成的,而是在查找過程中,當樹中不存在關鍵字等于給定值的結點時插入的。
插入過程如下:若二叉排序樹為空,則直接插入結點;若非空,先將給定的關鍵字與根結點的關鍵字進行比較,若小于根結點的關鍵字,則插入左子樹,若大于根結點的關鍵字,則插入右子樹。插入的結點一定是一個新添加的葉結點,且是查找失敗時的查找路徑上訪問的最后一個結點的左孩子或右孩子。
二叉排序樹的插入算法:
def BSTInsert(self, k):
TreeNode = self.RootNode
if TreeNode is None:
self.RootNode = BiTreeLinkNode(k)
return True
while True:
if k TreeNode.data:
if TreeNode.lchild is None:
TreeNode.lchild = BiTreeLinkNode(k)
return True
TreeNode = TreeNode.lchild
elif k > TreeNode.data:
if TreeNode.rchild is None:
TreeNode.rchild = BiTreeLinkNode(k)
return True
TreeNode = TreeNode.rchild
else:
return False
4. 二叉排序樹的構造
二叉排序樹的構造過程如下:從一棵空樹出發,依次輸入元素,將它們插入樹中的合適位置。關鍵字的序列不同,構造出來的二叉排序樹也會有所不同,比如下圖:

二叉排序樹的構造算法:
def CreateBST(self):
for val in self.data_list:
self.BSTInsert(val)
return self.RootNode
5. 二叉排序樹的刪除
在二叉排序樹中刪除一個結點時,不能把以該結點為根的子樹上的結點都刪除,必須先把被刪除的結點從存儲二叉排序樹的鏈表上摘下,將因刪除結點而斷開的二叉鏈表重新連接起來,同時確保二叉排序樹的性質不會丟失。具體分三種情況:
(1) 如果被刪除的結點是葉結點,可以直接刪除;
(2) 如果被刪除的結點只有一棵左子樹或右子樹,需要讓該結點的子樹成為該結點的父結點的子樹,以替代被刪除結點的位置;
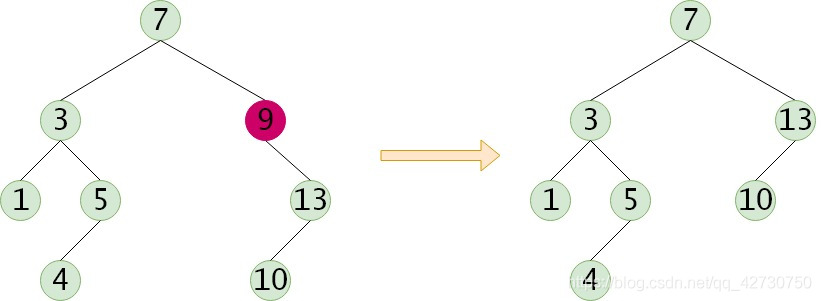
(3) 被刪除的結點有左子樹和右子樹,需要用該結點的直接后繼來代替該結點的位置,然后從二叉排序樹中刪去這個直接后繼。
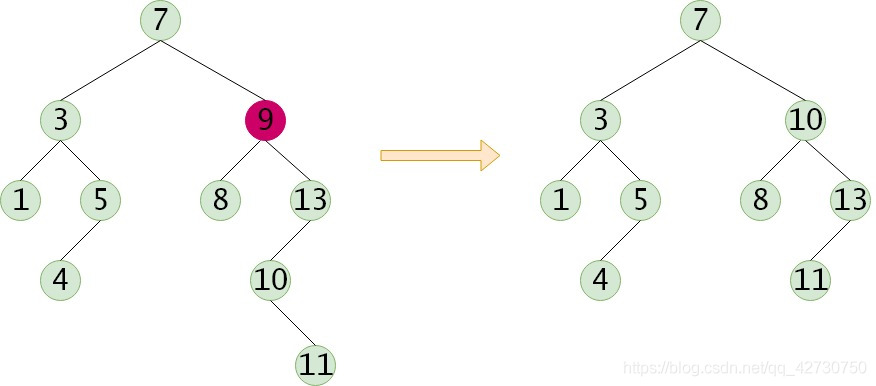
6. 二叉排序樹的查找效率分析
如果二叉排序樹的左、右子樹的高度之差的絕對值不超過1,則這樣的二叉樹稱為平衡二叉樹,它的平均查找長度為 O ( l o g 2 n ) O(log_2n) O(log2n);如果二叉排序樹是一個只有左子樹或右子樹的單支樹(類似于有序的單鏈表),則它的平均查找長度為 O ( n ) 。
在等概率情況下,有序列 { 2 , 1 , 4 , 3 }成的排序二叉樹的查找成功的平均查找長度為

有序列 { 1 , 2 , 3 , 4 } 構成的排序二叉樹的查找成功的平均查找長度為

二叉排序樹的查找效率主要取決于樹的高度,如果要提高查找效率,在構造二叉排序時最好不要使用有序的序列,盡量構造平衡二叉樹。
有關平均查找長度 A S L ASL ASL的知識會在查找這部分再說。
總結
到此這篇關于Python數據結構之二叉排序樹的定義、查找、插入、構造、刪除的文章就介紹到這了,更多相關Python二叉排序樹應用內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- Python 數據結構之樹的概念詳解
- python三種數據結構及13種創建方法總結
- python數據結構的排序算法
- Python內置數據結構列表與元組示例詳解
- Python二進制數據結構Struct的具體使用
- python用sqlacodegen根據已有數據庫(表)結構生成對應SQLAlchemy模型
- Python數據結構之圖的存儲結構詳解
- Python數據結構之優先級隊列queue用法詳解
- 詳解python數據結構之棧stack
- Python數據結構詳細