久久精品一区二区三区不卡,14表妺让我破了她的处

主頁 > 知識庫 > 圖文詳解matlab原始處理圖像幾何變換

圖文詳解matlab原始處理圖像幾何變換

（一）圖像幾何變換理論知識

（1）圖像的平移與比例

圖像的平移很簡單，平移前后的坐標分別為（x，y）和（x',y'）,則滿足的關系式為

x'= x +Tx；

y'= y +Ty；

其中Tx與Ty分別為對應的偏移量。

圖像的比例也很簡單，可以描述為：x'=S_x * x; y'=S_y * y;

那么上述的關系怎么用一個矩陣來表示呢？一個很重要的矩陣來了，那就是變換矩陣T，并且對于二維坐標下的點，一般轉化為笛卡爾坐標系下進行計算，用一個三維點表示二維的，只不過把最后一項值置為1，這樣一個二維坐標（x，y）就變為（x，y，1）了。在把上述的平移等式關系轉化為矩陣形式為：

比例等式關系為：

（2）關于旋轉變換

對于某個點，在坐標系中的變換為（旋轉角度為θ，并且逆時針旋轉為正）：

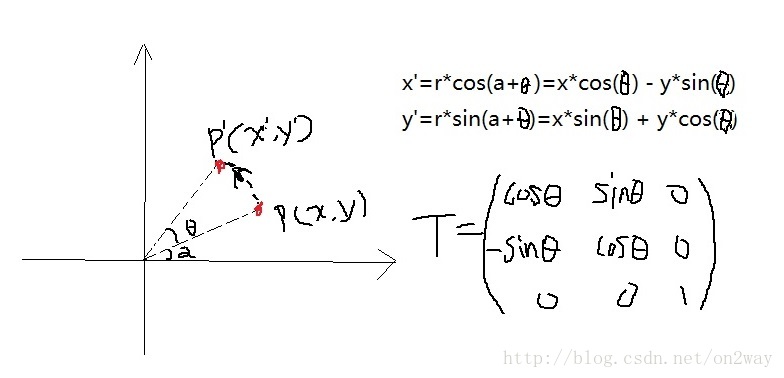
那么可以看出，這個時候對應的旋轉矩陣為T就如圖上所示。

（3）關于對稱變換

對稱變換比較簡單，還是以點的變換為例，比如變換前的點P（x，y）和變換后的點P'=（x',y'），那么對稱變換包括點關于x軸、y軸、原點、y=x、y=-x等等，點的變換可以自己推導下，這樣也就可以得到對應的變換矩陣T了。

比如，關于x對稱的話，T=[1,0,0;0,-1,0;0,0,1],關于原點對稱的話，T=[-1,0,0;0,-1,0;0,0,1];關于y=x對稱的話，T=[0,1,0;1,0,0;0,0,1];等等。

（4）復合變換

下面再重點介紹下復合變換，因為有的變換不是簡單的初等變換，但是有一點需要明確的是任何復合變換都可以用初等變換一步步變換而來。比如前面的旋轉變換，旋轉點選取的是原點，這樣才有的那個公式，那要是旋轉點不是原點怎么辦？比如任一點s（X_f,Y_f）,那么點P繞著點s旋轉一定的角度θ該怎么表示呢？這里就要把這個復合變換化成為3個簡單的初等變換，具體步驟為：首先把s點平移操作至原點（這個過程中，相當于所有的點都按照一定的方向平移了），然后相當于在原點對平移后的P點進行旋轉變換，變換完后再把這個店反平移回去，這樣是不是就相當于完成了那個復合變換。此時的變換矩陣為T，則T可以看出是兩次平移矩陣T1、T2和一次旋轉矩陣T3相乘的組合，即T=T1*T3*T2，注意方向不能反，因為是矩陣相乘，反的話相乘的結果不一定相同。

那么這個時候總的變換矩陣T就是：

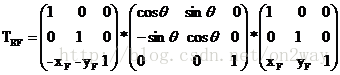
這個在編程實現原點移動位置時至關重要。

幾何變換的基礎知識就說到這，具體的可以再找相關文章了解。

（二）matlab編程實現變換

（1）對圖像的理解

Matlab表示一副圖像的方法很簡單，對于灰度圖像來說，就是一個二維矩陣，行與列存的就是像素點的位置，而矩陣值就是該像素點的灰度值。這里以有名的一副圖lenna圖為例，那么直接image=imread（‘lenna.jpg'）就可以加載帶matlab工作框中，顯示的話imshow（image）就可以了，顯示如下：

（2）比例變換

了解了變換的基本原理，要知道其中最重要的就是關于坐標的變換。如果以上圖中的行和列都為1的點作為原點的話，變換的程序為：

%-------------函數說明----------------
%    比例變換
%       輸入變量：img 灰白圖像（彩色不行）
%                s_x  x方向上的比例系數
%                s_y  y方向上的比例系數
%-------------------------------------
function bili(img,s_x,s_y)
[m,n] = size(img);
new_matrix = ones(m,n);
T1 = [s_x,0,0;0,s_y,0;0,0,1];   %對應的比例系數矩陣
for i=1:m
    for j=1:n
        p = floor([i,j,1]*T1^-1);%由P_new = P_old*T 可得：P_old = P_new*(T^-1)
        if (p(1)=m)(p(1)>0)(p(2)=n)(p(2)>0) %限制范圍 
         new_matrix(i,j) = img(p(1),p(2));   %坐標變換關系
        else 
        new_matrix(i,j) = 0;     %沒有的點賦值為0
        end
    end
end
figure;imshow(new_matrix,[]);
————————————————
版權聲明：本文為CSDN博主「on2way」的原創文章，遵循CC 4.0 BY-SA版權協議，轉載請附上原文出處鏈接及本聲明。
原文鏈接：https://blog.csdn.net/on2way/article/details/40460675

這樣運行對應程序：

bili（image,2,2）:

bili(image,0.5,0.5):

可以看到，分別對圖像擴大和縮小的時候，都是以行和列為1為原點來操作的。如果還是以這個點來進行旋轉操作的話，就會非常不協調不好看。況且如果了解matlab本身自帶這些旋轉、比例操作函數的話會發現，這些函數操作原點是圖像的正中心，這樣操作起來后才很好看。那么現在的問題就是如何把圖像的中心作為我們在坐標系下認為的原點呢？那就是上面講到的三步走了，首先平移中心點至原點，再變換，再平移至中心點就好了。我們需要做的就是確定平移的行與列的長度（平移的長度應該是圖像行與列總長度的一半吧，如果是把中心點當做原點的話）。基于此修改上述的程序如下：

function bili(img,s_x,s_y)
[m,n] = size(img);
new_matrix = ones(m,n);
T2 = [1,0,0;0,1,0;-m/2,-n/2,1];  %x、y軸平移值原點
T3 = [1,0,0;0,1,0;m/2,n/2,1];    %x、y軸反平移
 
T1 = [s_x,0,0;0,s_y,0;0,0,1];   %對應的比例系數矩陣
T = T2*T1*T3;     %P_new = P_old*T2*T1*T3  順序不能錯了
for i=1:m
    for j=1:n
        p = floor([i,j,1]*T1^-1);%由P_new = P_old*T 可得：P_old = P_new*(T^-1)
        if (p(1)=m)(p(1)>0)(p(2)=n)(p(2)>0) %限制范圍 
         new_matrix(i,j) = img(p(1),p(2));   %坐標變換關系
        else 
        new_matrix(i,j) = 0;     %沒有的點賦值為0
        end
    end
end
% figure;imshow(img,[]);
figure;imshow(new_matrix,[]);

從程序可以看出，只是多了那么兩個矩陣而已就可以實現原點的轉移了。

運行相應程序，bili（image,2,2）:

bili（image,0.5,0.5）:

可以看出，這樣操作以后是不是協調多了，基本上和matlab自帶的函數有相同的功能了。

（3）對稱變換

對稱變換和上述變換差不多，無非修改相應的變換矩陣，程序如下：

%-------------函數說明----------------
%    對稱變換
%       輸入變量：img 灰白圖像（彩色不行）
%                num 對稱類型
%     0：原點對稱，1：x軸對稱，2：y軸對稱
%     3：y=x軸對稱 4：y=-x軸對稱  其他。。
%-------------------------------------
function duichen(img,num)
[m,n] = size(img);
new_matrix = ones(m,n);
T2 = [1,0,0;0,1,0;-m/2,-n/2,1];  %x、y軸平移值原點
T3 = [1,0,0;0,1,0;m/2,n/2,1];    %x、y軸反平移
 
T_x = [1,0,0;0,-1,0;0,0,1];     %x軸對稱矩陣
T_y = [-1,0,0;0,1,0;0,0,1];     %y軸對稱矩陣
T_o = [-1,0,0;0,-1,0;0,0,1];    %原點對稱矩陣
T_yx = [0,1,0;1,0,0;0,0,1];     %y=x對稱的矩陣
T_xy = [0,-1,0;-1,0,0;0,0,1];   %y=-x對稱的矩陣
switch num                     %選擇某一種對稱方式
    case 0
        T = T2*T_o*T3 ;
    case 1
        T = T2*T_x*T3 ;
    case 2
        T = T2*T_y*T3 ;
    case 3
        T = T2*T_yx*T3 ;
    case 4
        T = T2*T_xy*T3 ;
end
for i=1:m                  %對于每一個像素點
    for j=1:n
        p = floor([i,j,1]*T^-1);%由P_new = P_old*T 可得：P_old = P_new*(T^-1)
        if (p(1)=m)(p(1)>0)(p(2)=n)(p(2)>0) %限制范圍 
         new_matrix(i,j) = img(p(1),p(2));   %坐標變換關系
        else 
        new_matrix(i,j) = 0;     %沒有的點賦值為0
        end
    end
end
% figure;imshow(img,[]);
figure;imshow(new_matrix,[]);
————————————————

運行相應程序：

>> duichen(image,0)

>> duichen(image,2)

（4）旋轉變換

%-------------函數說明----------------
%    旋轉變換
%       輸入變量：img 灰白圖像（彩色不行）
%                theat 變化的角度，逆時針旋轉為正             
%---------------------------------------
function xuanzhuan(img,theat)
[m,n] = size(img);
new_matrix = ones(m,n);
T2 = [1,0,0;0,1,0;-m/2,-n/2,1];  %x、y軸平移值原點
T3 = [1,0,0;0,1,0;m/2,n/2,1];    %x、y軸反平移
 
T1 = [cos(theat),sin(theat),0;-sin(theat),cos(theat),0;0,0,1];%旋轉變換
T = T2*T1*T3;                  %P_new = P_old*T2*T1*T3  順序不能錯了
for i=1:m
    for j=1:n
        p = floor([i,j,1]*T^-1);%由P_new = P_old*T 可得：P_old = P_new*(T^-1)
        if (p(1)=m)(p(1)>0)(p(2)=n)(p(2)>0) %限制范圍 
         new_matrix(i,j) = img(p(1),p(2));   %坐標變換關系
        else 
        new_matrix(i,j) = 0;     %沒有的點賦值為0
        end
    end
end
% figure;imshow(img,[]);
figure;imshow(new_matrix,[]);

運行相應程序：

>> xuanzhuan(image,pi/4)

>> xuanzhuan(image,-pi/3)

至此，一些基本的幾何變換操作就完成了，其他的變換就在次基礎上發揮了。

有一個問題是上述的變換在旋轉的時候，原圖的部分圖像會被切割掉，這個是沒有考慮到的，因為部分像素點在變換以后必然超出范圍，對比matlab自帶的旋轉函數可以發現自帶的函數是可以對出界的部分進行壓縮到范圍內。當然這一點我們也可以編程處理，不過稍微要麻煩點，必須對每個像素點再進行壓縮處理，這個有待研究。

二維圖像的幾何變換大致如此了。那么引申一下，對于三維圖像的幾何變換怎么處理了？其實歸結到底還是有一個變換矩陣T，而這個矩陣不再是3*3的了，這個時候增加了一維，那么對應的矩陣也得增加一維變成4*4的了，維數的增加必然帶來處理上的更加復雜了，不過理解了二維變換的原理，再來處理三維的話還是很好處理的，弄清楚對應關系就可以了。