久久精品国产精品成人片,男的操美女,国产精品久久久久久无码蜜臀漫画

主頁 > 知識庫 > Python學習之MRO方法搜索順序

Python學習之MRO方法搜索順序

為什么會講 MRO？

在講多繼承的時候，有講到，當繼承的多個父類擁有同名屬性、方法，子類對象調用該屬性、方法時會調用哪個父類的屬性、方法呢？
這就取決于 Python 的 MRO 了

什么是 MRO

MRO，method resolution order，方法搜索順序
對于單繼承來說，MRO 很簡單，從當前類開始，逐個搜索它的父類有沒有對應的屬性、方法
所以 MRO 更多用在多繼承時判斷方法、屬性的調用路徑
Python 中針對類提供了一個內置屬性__mro__可以查看方法搜索順序

實際代碼

class A:
    def test(self):
        print("AAA-test")


class B:
    def test(self):
        print("BBB-test")


# 繼承了三個類，B、A、還有默認繼承的 object
class C(B, A):
    ...


# 通過類對象調用，不是實例對象！
print(C.__mro__)

# 輸出結果
(class '__main__.C'>, class '__main__.B'>, class '__main__.A'>, class 'object'>)

1.在搜索方法時，是按照__mro__的輸出結果從左往右的順序查找的
2.如果在當前類（Class C）中找到方法，就直接執行，不再搜索
3.如果沒有找到，就查找下一個類中（Class B）是否有對應的方法，如果找到，就直接執行，不再搜素
4.如果找到最后一個類（Class object）都沒有找到方法，程序報錯

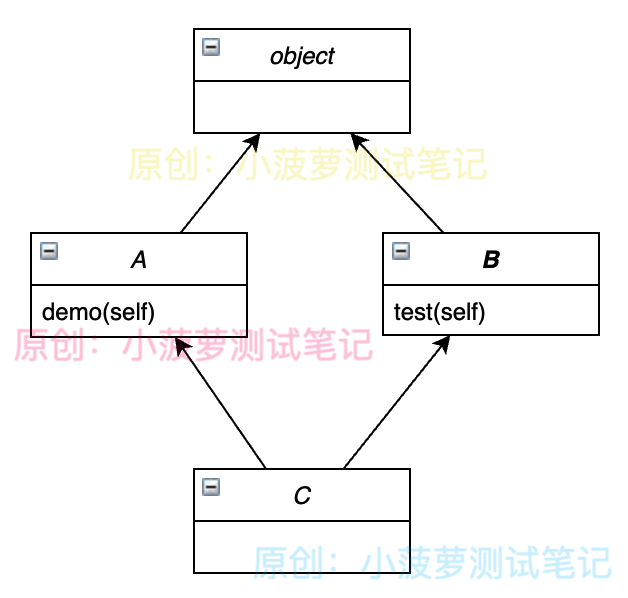
類圖

注意

其實 MRO 是涉及一個底層算法的，下面來詳細講解一下

MRO 算法

Python 發展到現在經歷了三種算法

舊式類 MRO 算法：從左往右，采用深度優先搜索（DFS），從左往右的算法，稱為舊式類的 MRO
新式類 MRO 算法：自 Python 2.2 版本開始，新式類在采用深度優先搜索算法的基礎上，對其做了優化
C3 算法：自 Python 2.3 版本，對新式類采用了 C3 算法；由于 Python 3.x 僅支持新式類，所以該版本只使用 C3 算法

什么是舊式類，新式類

Python學習之新式類和舊式類講解

想深入了解 C3 算法的可以看看官網

https://www.python.org/download/releases/2.3/mro/

舊式類 MRO 算法

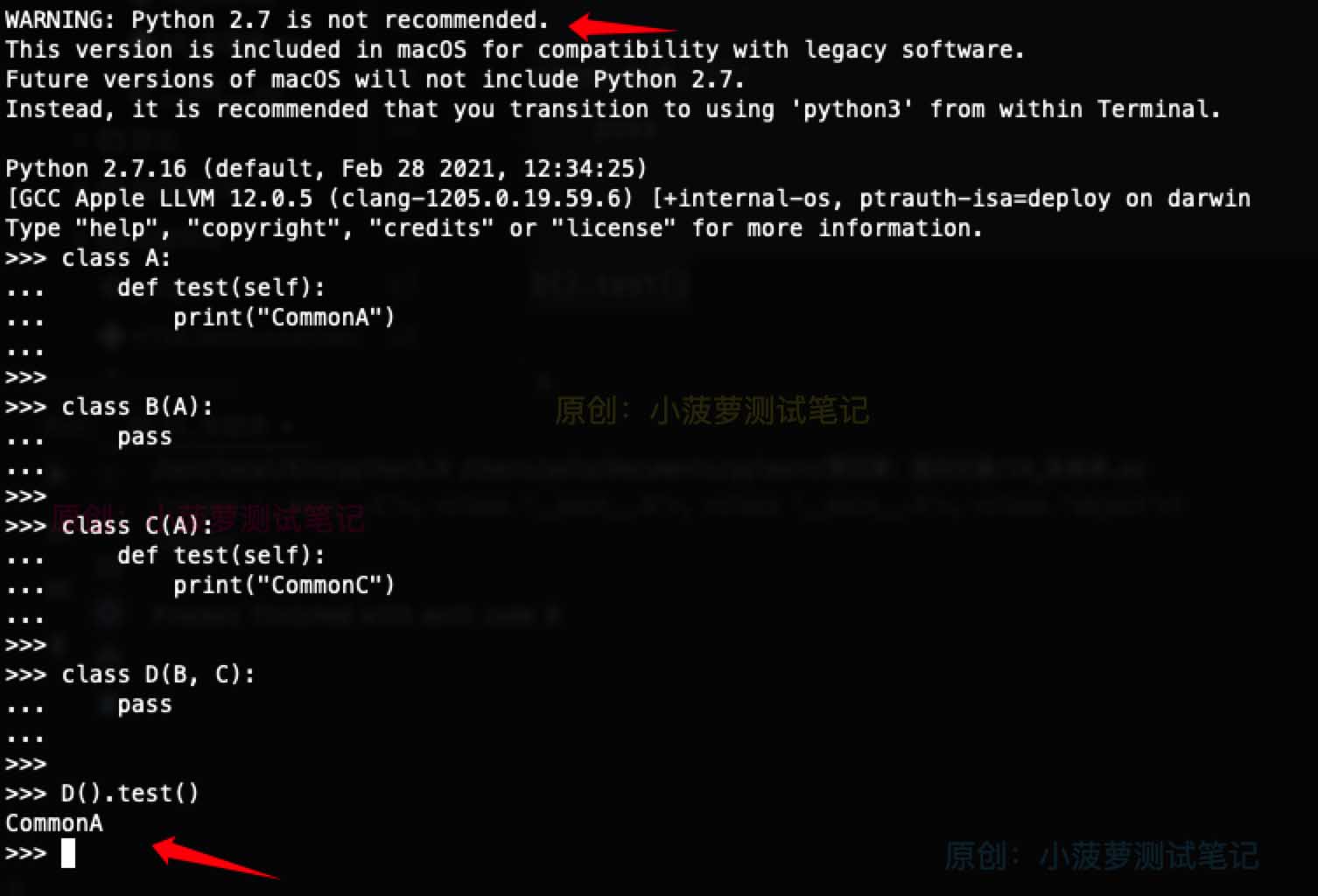
需要在 python2 環境下運行這段代碼

實際代碼

# 舊式類算法
class A:
    def test(self):
        print("CommonA")


class B(A):
    pass


class C(A):
    def test(self):
        print("CommonC")


class D(B, C):
    pass


D().test()

# python2 下的運行結果
CommonA

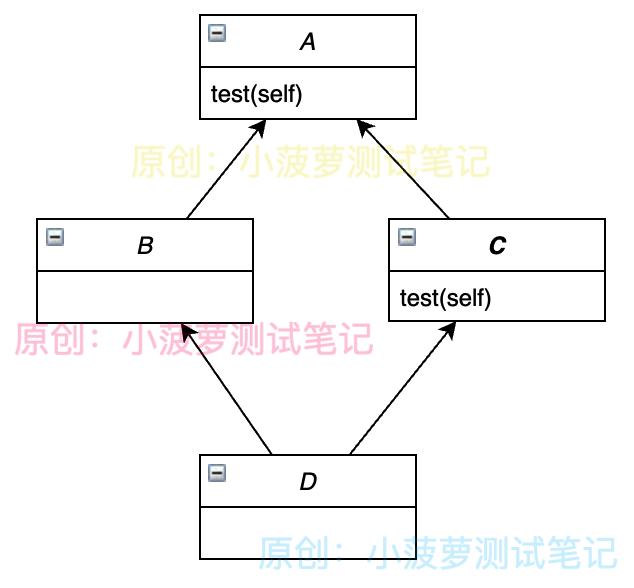
類圖

分析

通過類圖可以看到，此程序中的 4 個類是一個“菱形”繼承的關系
當使用 D 類實例對象訪問 test() 方法時，根據深度優先算法，搜索順序為D->B->A->C->A
因此，舊式類 MRO 算法最先搜索得到 test() 方法是在 A 類里面，所以最終輸出結果為 CommonA

新式類 MRO 算法

為解決舊式類 MRO 算法存在的問題，Python 2.2 版本推出了新的計算新式類 MRO 的方法
它仍然采用從左至右的深度優先遍歷，但是如果遍歷中出現重復的類，只保留最后一個

以上面的代碼栗子來講

深度優先遍歷，搜索順序為D->B->A->C->A
因為順序中有 2 個 A，因此只保留最后一個
最終搜索順序為D->B->C->A

新式 MRO 算法的問題

雖然解決了舊式 MRO 算法的問題，但可能會違反單調性原則

什么是單調性原則？

在子類存在多繼承時，子類不能改變父類的 MRO 搜索順序，否則會導致程序發生異常

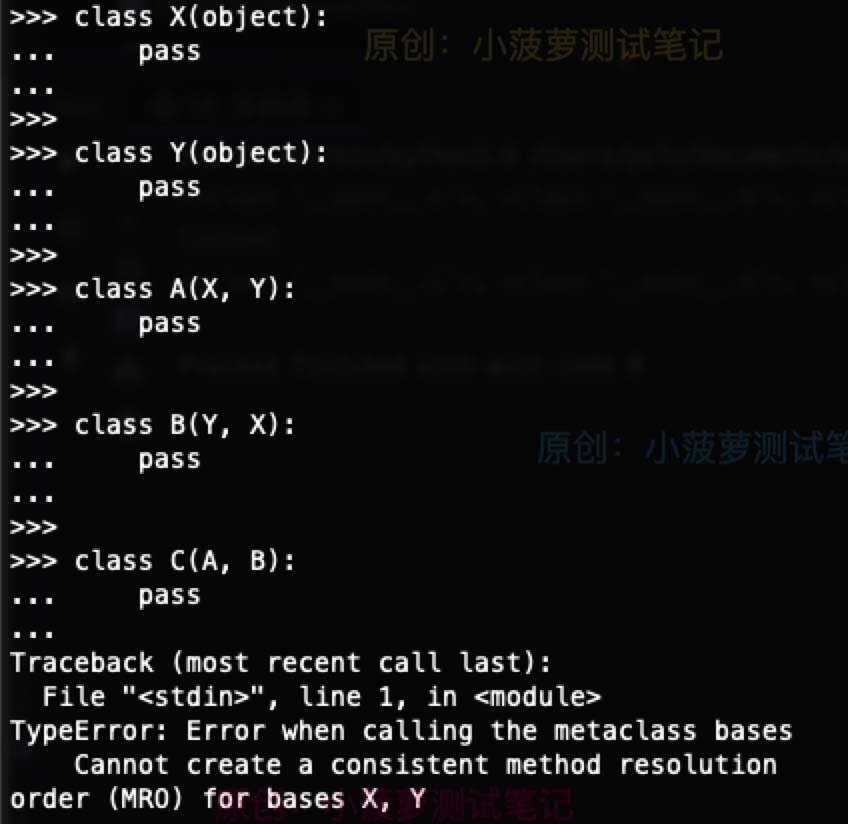
實際代碼

class X(object):
    pass


class Y(object):
    pass


class A(X, Y):
    pass


class B(Y, X):
    pass


class C(A, B):
    pass

深度優先遍歷后的搜索順序為：C->A->X->object->Y->object->B->Y->object->X->object

相同取后者的搜索順序為：C->A->B->Y->X->object

分析不同類的 MRO

A：A->X->Y->object
B：A->Y->X->object
C：C->A->B->X->Y->object

很明顯，B、C 中間的 X、Y 順序是相反的，就是說 B 被繼承時，它的搜索順序會被改變，違反了單調性

在 python2 中運行這段代碼的報錯

在 python3 中運行這段代碼的報錯

C3 MRO 算法

為解決前面兩個算法的問題，Python 2.3 采用了 C3 方法來確定方法搜索順序
多數情況下，如果別人提到 Python 中的 MRO，指的都是 C3 算法

將上面第一個栗子的代碼放到 python3 中運行

class A:
    def test(self):
        print("CommonA")


class B(A):
    pass


class C(A):
    def test(self):
        print("CommonC")


class D(B, C):
    pass


D().test()

# 輸出結果
CommonC

簡單了解下 C3 算法

以上面代碼為栗子，C3 會把各個類的 MRO 等價為以下等式

A：L[A] = merge(A , object)
B：L[B] = B + merge(L[A] , A)
C：L[C] = C + merge(L[A] , A)
D：L[D] = D + merge(L[B] , L[C] , B , C)

了解一下：頭、尾

以 A 類為栗，merge() 包含的 A 成為 L[A] 的頭，剩余元素（這里只有 object）稱為尾

merge 的運算方式

1.將merge 第一個列表的頭元素（如 L[A] 的頭），記作 H
2.如果 H 出現在 merge 其他列表的頭部，則將其輸出，并將其從所有列表中刪除
3.如果 H 只出現一次，那么也將其輸出，并將其從所有列表中刪除
4.如果 H 出現在 merge 其他列表的非頭部，則取下一個列表的頭元素記作 H，然后回到步驟二
5.最后回到步驟一，重復以上步驟

重復以上步驟直到列表為空，則算法結束；如果不能再找出可以輸出的元素，則拋出異常

簡單類 MRO 的計算栗子

class B(object): pass

print(B.__mro__)


(class '__main__.B'>, class 'object'>)

MRO 計算方式

L[B] = L[B(object)]
     = B + merge(L[object])
     = B + L[object]
     = B object

單繼承MRO 的計算栗子

# 計算 MRO
class B(object): pass

class C(B): pass

print(C.__mro__)


(class '__main__.C'>, class '__main__.B'>, class 'object'>)

MRO 計算方式

L[C] = C + merge(L[B])
     = C + L[B]
     = C B object

多繼承MRO 的計算栗子

O = object

class F(O): pass

class E(O): pass

class D(O): pass

class C(D, F): pass

class B(D, E): pass

class A(B, C): pass


print(C.__mro__)
print(B.__mro__)
print(A.__mro__)

# 輸出結果
(class '__main__.C'>, class '__main__.D'>, class '__main__.F'>, class 'object'>)
(class '__main__.B'>, class '__main__.D'>, class '__main__.E'>, class 'object'>)
(class '__main__.A'>, class '__main__.B'>, class '__main__.C'>, class '__main__.D'>, class '__main__.E'>, class '__main__.F'>, class 'object'>)

O 類、object 類 MRO 計算

L[O] = O = object

D、E、F 類 MRO 計算

L[D] = D + merge(L[O])
        = D O

C 類 MRO 計算

L[C] = L[C(D, F)]
     = C + merge(L[D], L[F], DF)
     # 從前面可知 L[D] 和 L[F] 的結果
     = C +  merge(DO, FO, DF)
     # 因為 D 是順序第一個并且在幾個包含 D 的 list 中是 head，
     # 所以這一次取 D 同時從列表中刪除 D
     = C + D + merge(O, FO, F)
     # 因為 O 雖然是順序第一個但在其他 list (FO)中是在尾部, 跳過
     # 改為檢查第二個list FO
     # F 是第二個 list 和其他 list 的 head
     # 取 F 同時從列表中刪除 F
     = C + D + F + merge(O)
     = C D F O

B 類 MRO 計算

L[B] = L[B(D, E)]
     = B + merge(L[D], L[E], DE)
     = B + merge(DO, EO, DE)
     = B + D + merge(O, EO, E)
     = B + D + E + merge(O)
     = B D E O

A 類 MRO 計算

L[A] = L[A(B,C)]
        = A + merge(L[B], L[C], BC)
        = A + merge( BDEO, CDFO, BC )
        = A + B + merge( DEO, CDFO, C )
        # D 在其他列表 CDFO 不是 head，所以跳過到下一個列表的 頭元素 C
        = A + B + C + merge( DEO, DFO )
        = A + B + C + D + merge( EO, FO )
        = A + B + C + D + E + merge( O, FO )
        = A + B + C + D + E + F + merge( O )
        = A B C D E F O

多繼承MRO 的計算栗子二

O = object

class F(O): pass

class E(O): pass

class D(O): pass

class C(D, F): pass

class B(E, D): pass

class A(B, C): pass


print(C.__mro__)
print(B.__mro__)
print(A.__mro__)

# 輸出結果
(class '__main__.C'>, class '__main__.D'>, class '__main__.F'>, class 'object'>)
(class '__main__.B'>, class '__main__.E'>, class '__main__.D'>, class 'object'>)
(class '__main__.A'>, class '__main__.B'>, class '__main__.E'>, class '__main__.C'>, class '__main__.D'>, class '__main__.F'>, class 'object'>)

O 類、object 類 MRO 計算

L[O] = O = object

D、E、F 類 MRO 計算

L[D] = D + merge(L[O])
        = D O

C 類 MRO 計算

L[C] = L[C(D, F)]
        = C + merge(L[D], L[F], DF)
        = C + merge(DO, FO, DF)
        = C + D + merge(O, FO, F)
        = C + D + F + merge(O)
        = C D F O

B 類 MRO 計算

L[B] = L[B(E, D)]
       = B + merge(L[E], L[D], ED)
       = B + merge(EO, DO, ED)
       = B + E + merge(O, DO, D)
       = B + E + D + merge(O)
       = B E D O

A 類 MRO 計算

L[A]  = L[A(B, C)]
        = A + merge(L[B], L[C], BC)
        = A + merge(BEDO, CDFO, BC)
        = A + B + merge(EDO, CDFO, C)
        = A + B + E + merge(DO,CDFO, C)
        = A + B + E + C + merge(O,DFO)
        = A + B + E + C + D + merge(O, FO)
        = A + B + E + C + D + F + merge(O)
        = A B E C D F O

到此這篇關于Python學習之MRO方法搜索順序的文章就介紹到這了,更多相關Python MRO方法搜索順序內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家！

您可能感興趣的文章: