目錄
- 一、K-means基礎算法簡介
- 二、算法過程
- 三、文字步驟
- 四、圖形展示
- 五、代碼實現
- 六、小結
一、K-means基礎算法簡介
k-means算法是一種聚類算法,所謂聚類,即根據相似性原則,將具有較高相似度的數據對象劃分至同一類簇,將具有較高相異度的數據對象劃分至不同類簇。聚類與分類最大的區別在于,聚類過程為無監督過程,即待處理數據對象沒有任何先驗知識,而分類過程為有監督過程,即存在有先驗知識的訓練數據集。
二、算法過程
K-means中心思想:事先確定常數K,常數K意味著最終的聚類(或者叫簇)類別數,首先隨機選定初始點為質心,并通過計算每一個樣本與質心之間的相似度(這里為歐式距離),將樣本點歸到最相似的類中,接著,重新計算每個類的質心(即為類中心),重復這樣的過程,直到質心不再改變,最終就確定了每個樣本所屬的類別以及每個類的質心。由于每次都要計算所有的樣本與每一個質心之間的相似度,故在大規模的數據集上,K-Means算法的收斂速度比較慢。
1.聚類算法:
是一種典型的無監督學習算法,主要用于將相似的樣本自動歸到一個類別中。
聚類算法與分類算法最大的區別是:聚類算法是無監督的學習算法,而分類算法屬于監督的學習
算法,分類是知道結果的。
在聚類算法中根據樣本之間的相似性,將樣本劃分到不同的類別中,對于不同的相似度計算方法,會得到不同的聚類結果,常用的相似度計算方法有歐式距離法。
2.聚類:
物理或抽象對象的集合分成由類似的對象組成的多個類的過程被稱為聚類。由聚類所生成的簇是一組數據對象的集合,這些對象與同一個簇中的對象彼此相似,與其他簇中的對象相異。
3.簇:
本算法中可以理解為,把數據集聚類成 k 類,即 k 個簇。
4.質心:
指各個類別的中心位置,即簇中心。
5.距離公式:
常用的有:歐幾里得距離(歐氏距離)、曼哈頓距離、閔可夫斯基距離等。
三、文字步驟
1.給定一個待處理的數據集
2.選擇簇的個數k(kmeans算法傳遞超參數的時候,只需設置最大的K值)
3.任意產生k個簇,生成K個簇的中心,記 K 個簇的中心分別為 c 1 , c 2 , . . . , c k c1,c2,...,ck c1,c2,...,ck;每個簇的樣本數量為 N 1 , N 2 , . . . , N 3 N1,N2,...,N3 N1,N2,...,N3。
4.通過歐幾里得距離公式計算各點到各質心的距離,把每個點劃分給與其距離最近的質心,從而初步把數據集分為了 K 類點。
5.更新質心:通過下面的公式來更新每個質心。就是,新的質心的值等于當前該質心所屬簇的所有點的平均值。 c j = 1 N j ∑ i = 1 N j x i , y i c_{j}=\frac{1}{N_{j}}\sum_{i=1}^{N{j}}x_{i},y_{i} cj=Nj1i=1∑Njxi,yi
6.重復以上步驟直到滿足收斂要求。(通常就是確定的中心點不再改變。)
四、圖形展示
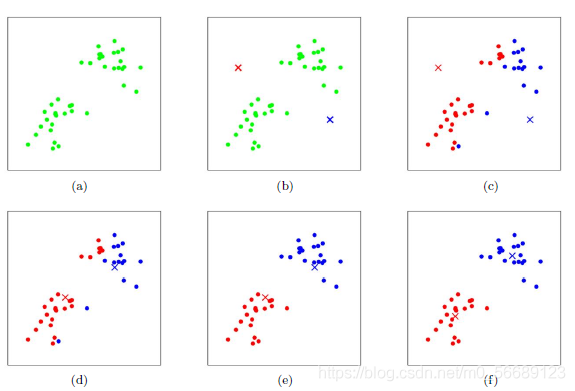
按照上述步驟我們可以更好地理解分類過程;
五、代碼實現
x 軸數據],[存儲 y 軸數據]]
for i in range(m):
if i m/3:
data[0].append(uniform(1,5))#隨機設定
data[1].append(uniform(1,5))
elif i 2*m/3:
data[0].append(uniform(6,10))
data[1].append(uniform(1,5))
else:
data[0].append(uniform(3,8))
data[1].append(uniform(5,10))
#將創建的數據集畫成散點圖
plt.scatter(data[0],data[1])
plt.xlim(0,11)
plt.ylim(0,11)
plt.show()
#定義歐幾里得距離
def distEuclid(x1,y1,x2,y2):
d = sqrt((x1-x2)**2+(y1-y2)**2)
return d
cent0 = [uniform(2,9),uniform(2,9)] #定義 K=3 個質心,隨機賦值
cent1 = [uniform(2,9),uniform(2,9)] #[x,y]
cent2 = [uniform(2,9),uniform(2,9)]
mark = [] #標記列表
dist = [[],[],[]]#各質心到所有點的距離列表
#核心
for n in range(50):
#計算各質心到所有點的距離
for i in range(m):
dist[0].append(distEuclid(cent0[0],cent0[1],data[0][i],data[1][i]))
dist[1].append(distEuclid(cent1[0],cent1[1],data[0][i],data[1][i]))
dist[2].append(distEuclid(cent2[0],cent2[1],data[0][i],data[1][i]))
#對數據進行整理
sum0_x = sum0_y = sum1_x = sum1_y = sum2_x = sum2_y = 0
number0 = number1 = number2 = 0
for i in range(m):
if dist[0][i]dist[1][i] and dist[0][i]dist[2][i]:
mark.append(0)
sum0_x += data[0][i]
sum0_y += data[1][i]
number0 += 1
elif dist[1][i]dist[0][i] and dist[1][i]dist[2][i]:
mark.append(1)
sum1_x += data[0][i]
sum1_y += data[1][i]
number1 += 1
elif dist[2][i]dist[0][i] and dist[2][i]dist[1][i]:
mark.append(2)
sum2_x += data[0][i]
sum2_y += data[1][i]
number2 += 1
#更新質心
cent0 = [sum0_x/number0,sum0_y/number0]
cent1 = [sum1_x/number1,sum1_y/number1]
cent2 = [sum2_x/number2,sum2_y/number2]
#畫圖
for i in range(m):
if mark[i] == 0:
plt.scatter(data[0][i],data[1][i],color='red')
if mark[i] == 1:
plt.scatter(data[0][i],data[1][i],color='blue')
if mark[i] == 2:
plt.scatter(data[0][i],data[1][i],color='green')
plt.scatter(cent0[0],cent0[1],marker='*',color='red')
plt.scatter(cent1[0],cent1[1],marker='*',color='blue')
plt.scatter(cent2[0],cent2[1],marker='*',color='green')
plt.xlim(0,11)
plt.ylim(0,11)
plt.show()
在這里插入代碼片
上述代碼數據選擇是隨機生成的,每次運行結果是不同的,測試會發現出現分類不理想的效果。說明基礎算法存在很大的弊端,我們需要改進,本篇內容為基礎不做改進知識的說明。
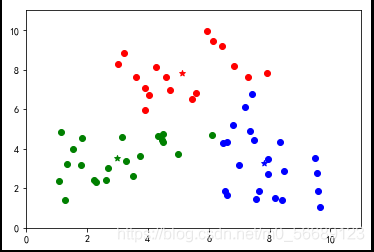
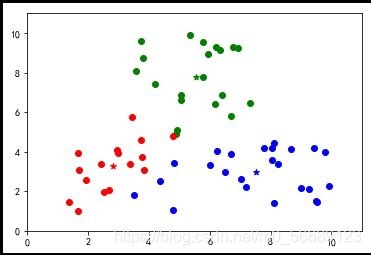
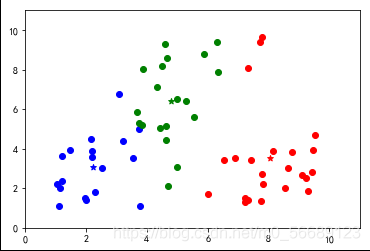
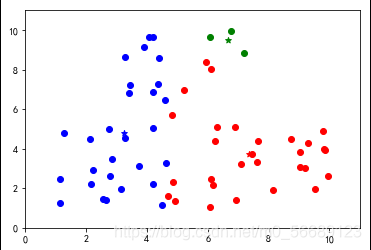
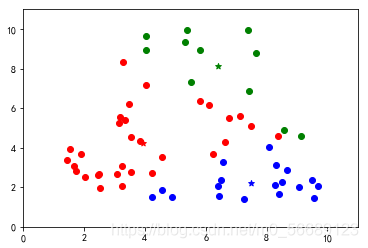
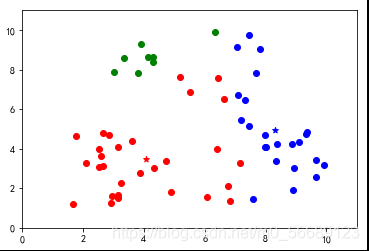
六、小結
優點
算法簡單易實現;
聚類效果依賴K值選定,
缺點
需要用戶事先指定類簇個數;
聚類結果對初始類簇中心的選取較為敏感;
容易陷入局部最優; 只能發現球形類簇;
到此這篇關于Python機器學習之Kmeans基礎算法的文章就介紹到這了,更多相關Python Kmeans基礎算法內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- Python 機器學習工具包SKlearn的安裝與使用
- Python機器學習之KNN近鄰算法
- Python機器學習算法之決策樹算法的實現與優缺點
- Python機器學習三大件之一numpy
- Python機器學習之決策樹
- python機器學習之線性回歸詳解
- python 機器學習的標準化、歸一化、正則化、離散化和白化
- Python機器學習工具scikit-learn的使用筆記
- python機器學習庫xgboost的使用
- python機器學習實現決策樹
- python機器學習包mlxtend的安裝和配置詳解
- Python機器學習算法庫scikit-learn學習之決策樹實現方法詳解
- Python機器學習之基礎概述