BN與Dropout共同使用出現的問題
BN和Dropout單獨使用都能減少過擬合并加速訓練速度,但如果一起使用的話并不會產生1+1>2的效果,相反可能會得到比單獨使用更差的效果。
相關的研究參考論文:Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift
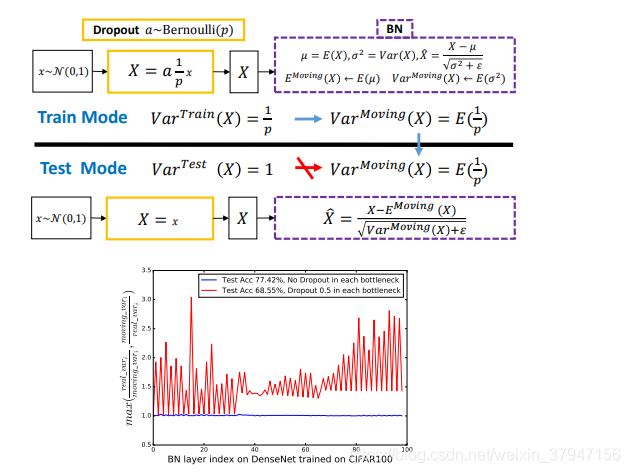
本論文作者發現理解 Dropout 與 BN 之間沖突的關鍵是網絡狀態切換過程中存在神經方差的(neural variance)不一致行為。
試想若有圖一中的神經響應 X,當網絡從訓練轉為測試時,Dropout 可以通過其隨機失活保留率(即 p)來縮放響應,并在學習中改變神經元的方差,而 BN 仍然維持 X 的統計滑動方差。
這種方差不匹配可能導致數值不穩定(見下圖中的紅色曲線)。
而隨著網絡越來越深,最終預測的數值偏差可能會累計,從而降低系統的性能。
簡單起見,作者們將這一現象命名為「方差偏移」。
事實上,如果沒有 Dropout,那么實際前饋中的神經元方差將與 BN 所累計的滑動方差非常接近(見下圖中的藍色曲線),這也保證了其較高的測試準確率。
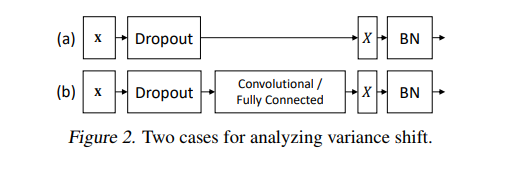
作者采用了兩種策略來探索如何打破這種局限。
一個是在所有 BN 層后使用 Dropout,另一個就是修改 Dropout 的公式讓它對方差并不那么敏感,就是高斯Dropout。
第一個方案比較簡單
把Dropout放在所有BN層的后面就可以了,這樣就不會產生方差偏移的問題,但實則有逃避問題的感覺。
第二個方案
來自Dropout原文里提到的一種高斯Dropout,是對Dropout形式的一種拓展。作者進一步拓展了高斯Dropout,提出了一個均勻分布Dropout,這樣做帶來了一個好處就是這個形式的Dropout(又稱為“Uout”)對方差的偏移的敏感度降低了,總得來說就是整體方差偏地沒有那么厲害了。
BN、dropout的幾個問題和思考
1、BN的scale初始化
scale一般初始化為1.0。
聯想到權重初始化時,使用relu激活函數時若采用隨機正太分布初始化權重的公式是sqrt(2.0/Nin),其中Nin是輸入節點數。即比一般的方法大了2的平方根(原因是relu之后一半的數據變成了0,所以應乘以根號2)。
那么relu前的BN,是否將scale初始化為根號2也會加速訓練?
這里主要有個疑點:BN的其中一個目的是統一各層的方差,以適用一個統一的學習率。那么若同時存在sigmoid、relu等多種網絡,以上方法會不會使得統一方差以適應不同學習率的效果打了折扣?
沒來得及試驗效果,如果有試過的朋友請告知下效果。
2、dropout后的標準差改變問題
實踐發現droput之后改變了數據的標準差(令標準差變大,若數據均值非0時,甚至均值也會產生改變)。
如果同時又使用了BN歸一化,由于BN在訓練時保存了訓練集的均值與標準差。dropout影響了所保存的均值與標準差的準確性(不能適應未來預測數據的需要),那么將影響網絡的準確性。
若輸入數據為正太分布,只需要在dropout后乘以sqrt(0.5)即可恢復原來的標準差。但是對于非0的均值改變、以及非正太分布的數據數據,又有什么好的辦法解決呢?
3、稀疏自編碼的稀疏系數
稀疏自編碼使用一個接近0的額外懲罰因子來使得隱層大部分節點大多數時候是抑制的,本質上使隱層輸出均值為負數(激活前),例如懲罰因子為0.05,對應sigmoid的輸入為-3.5,即要求隱層激活前的輸出中間值為-3.5,那么,是不是可以在激活前加一層BN,beta設為-3.5,這樣學起來比較快?
經過測試,的確將BN的beta設為負數可加快訓練速度。因為網絡初始化時就是稀疏的。
但是是不是有什么副作用,沒有理論上的研究。
4、max pooling是非線性的,avg pooling是線性的
總結
以上為個人經驗,希望能給大家一個參考,也希望大家多多支持腳本之家。
您可能感興趣的文章:- 解決Pytorch中的神坑:關于model.eval的問題
- 聊聊pytorch測試的時候為何要加上model.eval()
- pytorch:model.train和model.eval用法及區別詳解