目錄
- 什么是決策樹
- 決策樹組成
- 節點的確定方法
- 決策樹基本流程
- 決策樹的常用參數
- 代碼實現決策樹之分類樹
- 網格搜索在分類樹上的應用
- 分類樹在合成數據的表現
- 什么是隨機森林
- 隨機森林的原理
- 隨機森林常用參數
- 決策樹和隨機森林效果
- 實例用隨機森林對乳腺癌數據的調參
什么是決策樹
決策樹屬于經典的十大數據挖掘算法之一���,是通過類似于流程圖的數形結構���,其規則就是iIF…THEN…的思想.,可以用于數值型因變量的預測或離散型因變量的分類�,該算法簡單直觀��,通俗易懂����,不需要研究者掌握任何領域的知識或者復雜的數學邏輯�,而且算法的輸出結果具有很強的解釋性,通常情況下決策術用作分類器會有很好的預測準確率��,目前越來越多的行業�����,將此算法用于實際問題的解決����。
決策樹組成

這就是一個典型的決策樹����,其呈現字頂向下生長的過程��,通過樹形結構可以將數據中的隱藏的規律����,直觀的表現出來���,圖中深色的橢圓表示樹的根節點檢測的為橢圓表示樹的中間節點�,方框表示數的葉子節點,對于所有非葉子節點來說都是用于條件判斷,葉節點則表示最終儲存的分類結果。
- 根節點:沒有進邊,有出邊����。包含最初的���,針對特征的提問�。
- 中間節點:既有進邊也有出邊�����,進邊只有一條����,出邊可以有很多條�。都是針對特征的提問。
- 葉子節點:有進邊�����,沒有出邊����,每個葉子節點都是一個類別標簽�����。
- 子節點和父節點:在兩個相連的節點中��,更接近根節點的是父節點,另一個是子節點�。
節點的確定方法
那么對于所有的非葉子節點的字段的選擇����,可以直接決定我們分類結果的好和壞��,那么如何使這些非葉子節點分類使結果更好和效率更高�,也就是我們所說的純凈度��,對于純凈度的衡量��,我們有三個衡量指標信息增益�����,信息增益率和基尼系數。
- 對于信息增益來說�,就是在我們分類的過程中�����,會對每一種分類條件的結果都會進行信息增益量的的計算。然后通過信息增益的比較取出最大的信息增益對應的分類條件���。也就是說對于信息增益值最大的量就是我們尋找的最佳分類條件。關于信息增益值是怎么計算得出的����,這里就不做過多的講解����,因為它需要基于大量的數學計算和概率知識���。)輸入”entropy“��,使用信息熵(Entropy)
- 在計算信息增益的過程中,可能會受到數據集類別效果不同的值過多�,所以會造成信息增益的計算結果將會更大���,但是有時候并不能夠真正體現我們數據集的分類效果�,所以這里引入信息增益率來對于信息增益值進行一定程度的懲罰����,簡單的理解就是將信息增益值除以信息量。
- 決策樹中的信息增益率和信息增益指標實現根節點和中間節點的選擇����,只能針對離散型隨機變量進行分類�����,對于連續性的因變量就束手無策,為了能夠讓決策數預測連續性的因變量�����,所以就引入了基尼系數指標進行字段選擇特征���。輸入”gini“���,使用基尼系數(Gini Impurity)
比起基尼系數�,信息熵對不純度更加敏感,對不純度的懲罰最強�����。但是在實際使用中�����,信息熵和基尼系數的效果基本相同。信息熵的計算比基尼系數緩慢一些,因為基尼系數的計算不涉及對數����。另外�����,因為信息熵對不純度更加敏感,所以信息熵作為指標時,決策樹的生長會更加“精細”,因此對于高維數據或者噪音很多的數據,信息熵很容易過擬合�����,基尼系數在這種情況下效果往往比較好���。
決策樹基本流程

他會循環次過程,直到沒有更多的特征可用,或整體的不純度指標已經最優���,決策樹就會停止生長。但是在建模的過程中可能會由于這種高精度的訓練,使得模型在訓練基礎上有很高的預測精度,但是在測試集上效果并不夠理想,為了解決過擬合的問題,通常會對于決策樹進行剪枝操作����。
對于決策樹的剪枝操作有三種:誤差降低剪枝法�,悲觀剪枝法�,代價復雜度剪枝法,但是在這里我們只涉及sklearn中����,給我們提供的限制決策樹生長的參數��。
決策樹的常用參數
DecisionTreeClassifier(criterion="gini"
# criterion用于指定選擇節點字段的評價指標�。對于分類決策樹默認gini,表示采用基尼系數指標進行葉子節點的最佳選擇?�?捎小癳ntropy”,但是容易過擬合���,用于擬合不足
# 對于回歸決策數�,默認“mse”,表示均方誤差選擇節點的最佳分割手段。
,random_state=None
# 用于指定隨機數生成器的種子�����,默認None表示使用默認的隨機數生成器����。
,splitter="best"
# 用于指定節點中的分割點的選擇方法,默認best表示從所有的分割點中選出最佳分割點�,
# 也可以是random�,表示隨機選擇分割點
#以下參數均為防止過擬合
,max_depth=None
# 用于指定決策樹的最大深度�,默認None,表示樹的生長過程中對于深度不做任何限制���。
,min_samples_leaf=1
# 用于指定葉節點的最小樣本量默認為1。
,min_samples_split=2
# 用于指定根節點或中間節點能夠繼續分割的最小樣本量默認為2���。
,max_features=None
# 用于指定決策樹包含的最多分隔字段數,默認None表示分割時使用所有的字段���。如果為具體的整數,則考慮使用對應的分割手段數,如果為0~1的浮點數���,則考慮對于對應百分比的字段個數。
,min_impurity_decrease=0
# 用于指定節點是否繼續分割的最小不純度值,默認為0
,class_weight=None
# 用于指定因變量中類別之間的權重。默認None表示每個類別的權重都相同��。
)
代碼實現決策樹之分類樹
import pandas as pd
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_wine
import graphviz
# 實例化數據集�����,為字典格式
wine=load_wine()
datatarget=pd.concat([pd.DataFrame(wine.data),pd.DataFrame(wine.target)],axis=1)
# 通過數據集的數據和標簽進行訓練和測試集的分類。
xtrain,xtest,ytrain,ytest=train_test_split(wine.data # 數據集的數據�。
,wine.target# 數據集標簽���。
,test_size=0.3#表示訓練集為70%測試集為30%����。
)
# 創建一個樹的模型�����。
clf=tree.DecisionTreeClassifier(criterion="gini") # 這里只使用了基尼系數作為參數�����,其他沒有暫時使用
# 將訓練集數據放在模型中進行訓練,clf就是我們訓練好的模型���,可以用來進行測試劑的決策。
clf=clf.fit(xtrain,ytrain)
# 那么對于我們訓練好的模型來說�,怎么樣才能夠說明他是一個比較好的模型�����,那么我們就要引入模型中的一個函數score進行模型打分
clf.score(xtest,ytest)#測試集打分
# 也可以使用交叉驗證的方式,對于數據進行評估更具有穩定性����。
cross_val_score(clf # 填入想要打分的模型����。
,wine.data# 打分的數據集
,wine.target# 用于打分的標簽。
,cv=10# 交叉驗證的次數
#,scoring="neg_mean_squared_error"
#只有在回歸中有該參數���,表示以負均方誤差輸出分數
).mean()
# 將決策樹以樹的形式展現出來
dot=tree.export_graphviz(clf
#,feature_names #特征名
#,class_names #結果名
,filled=True#顏色自動填充
,rounded=True)#弧線邊界
graph=graphviz.Source(dot)
# 模型特征重要性指標
clf.feature_importances_
#[*zip(wine.feature_name,clf.feature_importances_)]特征名和重要性結合
#apply返回每個測試樣本所在的葉子節點的索引
clf.apply(Xtest)
#predict返回每個測試樣本的分類/回歸結果
clf.predict(Xtest)
決策樹不同max_depth的學習曲線
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_wine
import matplotlib.pyplot as plt、
wine=load_wine()
xtrain,xtest,ytrain,ytest=train_test_split(wine.data,wine.target,test_size=0.3)
trainscore=[]
testscore=[]
for i in range(10):
clf=tree.DecisionTreeClassifier(criterion="gini"
,random_state=0
,max_depth=i+1
,min_samples_split=5
,max_features=5
).fit(xtrain,ytrain)
# 下面這這兩句代碼本質上結果是一樣的�。第2種比較穩定,但是費時間
once1=clf.score(xtrain,ytrain)
once2=cross_val_score(clf,wine.data,wine.target,cv=10).mean()#也可用clf.score(xtest,ytest)
trainscore.append(once1)
testscore.append(once2)
#畫圖像
plt.plot(range(1,11),trainscore,color="red",label="train")
plt.plot(range(1,11),testscore,color="blue",label="test")
#顯示范圍
plt.xticks(range(1,11))
plt.legend()
plt.show()
result:
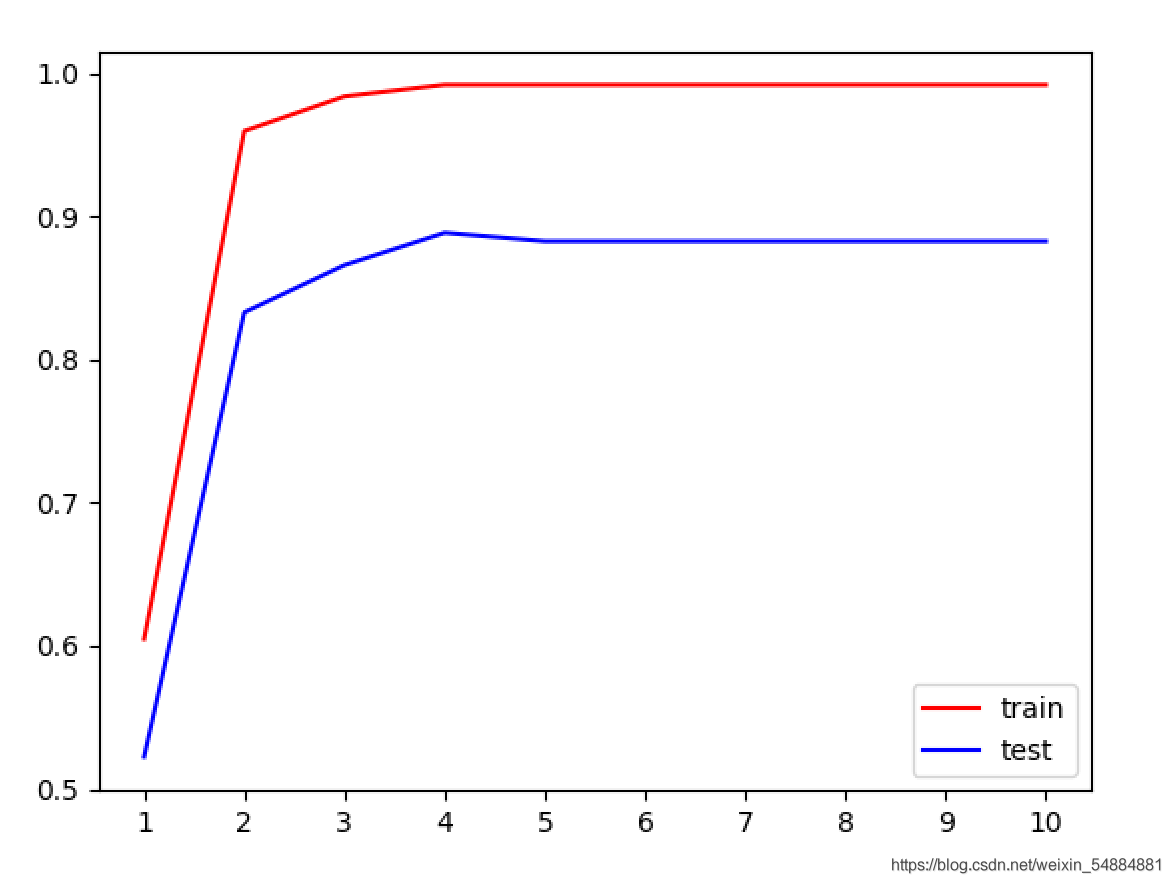
一般情況下���,隨著max_depth的升高訓練集和測試集得分就相對越高,但是由于紅酒數據集的數據量比較少��,并沒有特別明顯的體現出來�。但是我們依舊可以看出:在最大深度為4的時候到達了測試級的效果巔峰。
網格搜索在分類樹上的應用
我們發現對于這個模型的參數比較多��,如果我們想要得到一個相對來說分數比較高的效果比較好的模型的話�����,我們需要對于每一個參數都要進行不斷的循環遍歷��,最后才能夠得出最佳答案。但是這對于我們人為的實現來說比較困難���,所以我們有了這樣一個工具:網格搜索可以自動實現最佳效果的各種參數的確定。(但是比較費時間)
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
from sklearn.model_selection import GridSearchCV # 網格搜索的導入
wine = load_wine()
xtrain, xtest, ytrain, ytest = train_test_split(wine.data, wine.target, test_size=0.3)
clf = DecisionTreeClassifier(random_state=0) # 確定random_state,就會在以后多次運行的情況下結果相同
# parameters為網格搜索的主要參數�����,它是以字典的形式存在�。鍵為指定模型的參數名稱,值為參數列表
parameters = {"criterion": ["gini", "entropy"]
, "splitter": ["best", "random"]
, "max_depth": [*range(1, 10)]
# ,"min_samples_leaf":[*range(5,10)]
}
# 使用網絡搜索便利查詢,返回建立好的模型�����,網格搜索包括交叉驗證cv為交叉次數
GS = GridSearchCV(clf, cv=10, param_grid=parameters)
# 進行數據訓練
gs = GS.fit(xtrain, ytrain)
# best_params_接口可以查看最佳組合
# 最佳組合����,(不一定最好,可能有些參數不涉及結果更好)
best_choice = gs.best_params_
print(best_choice)
# best_score_接口可以查看最佳組合的得分
best_score = gs.best_score_
print(best_score)
回歸樹中不同max_depth擬合正弦函數數據
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
#隨機數生成器的實例化
rng = np.random.RandomState(0)
# rng.rand(80, 1)在0到1之間生成80個數��,axis=0�,縱向排序作為自變量
X = np.sort(5 * rng.rand(80, 1), axis=0)
# 因變量的生成
y = np.sin(X).ravel()
# 添加噪聲
y[::5] += 3 * (0.5 - rng.rand(16))
#建立不同樹模型,回歸樹除了criterion其余和分類樹參數相同
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
# 訓練數據
regr_1.fit(X, y)
regr_2.fit(X, y)
# 生成測試數據
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
# 預測X_test數據在不同數上的表現
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
#畫圖
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black",
c="red", label="data")
plt.plot(X_test, y_1, color="blue",
label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="green", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
結果:
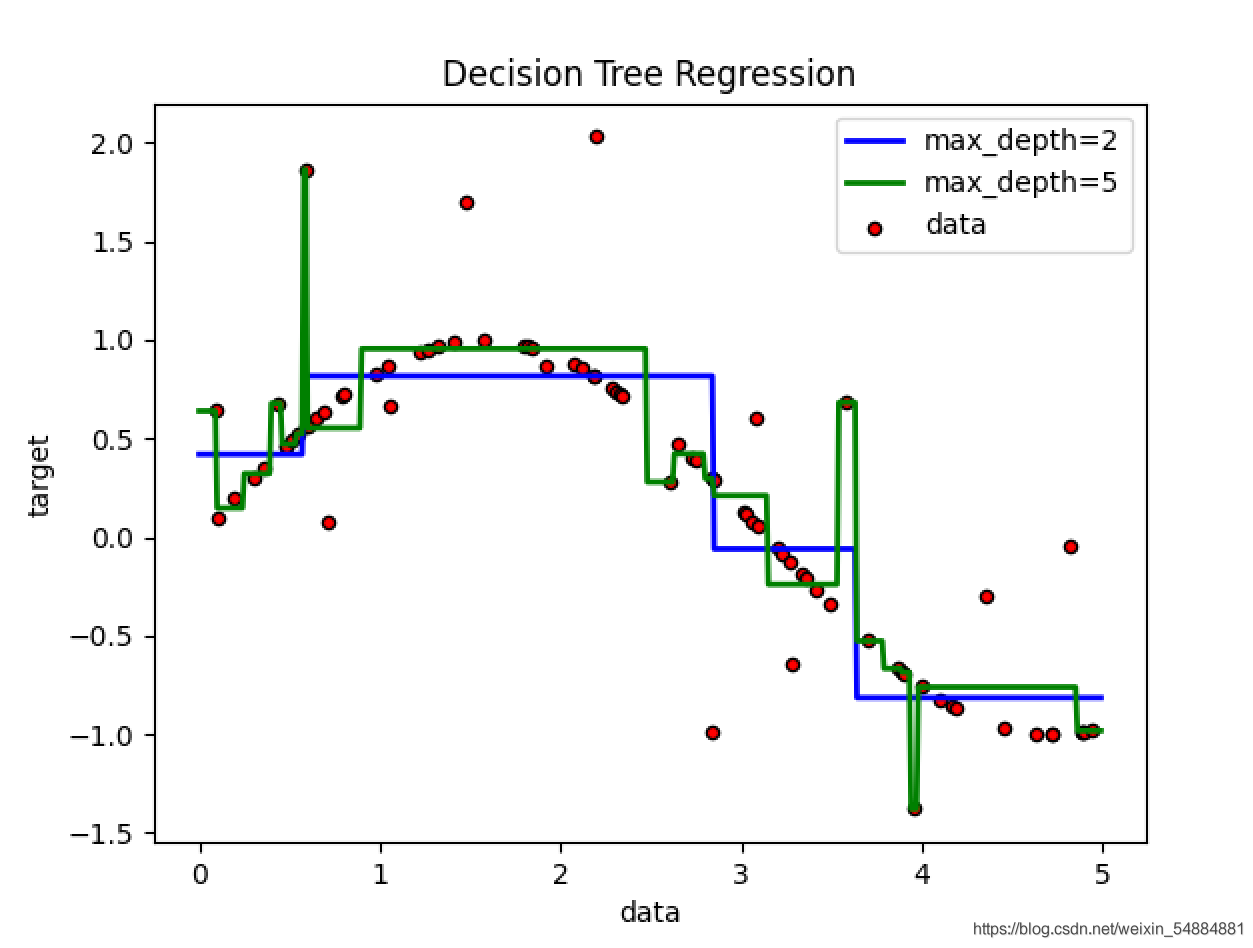
從圖像可以看出對于不同深度的節點來說�,有優點和缺點��。對于max_depth=5的時候��,一般情況下很貼近原數據結果����,但是對于一些特殊的噪聲來說�����,也會非常貼近噪聲���,所以在個別的點的地方會和真實數據相差比較大�����,也就是過擬合現象(對于訓練數據集能夠很好地判斷出出,但是對于測試數據集來說結果并不理想)。對于max_depth=2的時候���,雖然不能夠特別貼近大量的數據集,但是在處理一些噪聲的時候,往往能夠很好的避免����。
分類樹在合成數據的表現
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.tree import DecisionTreeClassifier
######生成三種數據集######
# 二分類數據集
X, y = make_classification(n_samples=100, #生成100個樣本
n_features=2,#有兩個特征
n_redundant=0, #添加冗余特征0個
n_informative=2, #包含信息的特征是2個
random_state=1,#隨機模式1
n_clusters_per_class=1 #每個簇內包含的標簽類別有1個
)
rng = np.random.RandomState(2) #生成一種隨機模式
X += 2 * rng.uniform(size=X.shape) #加減0~1之間的隨機數
linearly_separable = (X, y) #生成了新的X����,依然可以畫散點圖來觀察一下特征的分布
#plt.scatter(X[:,0],X[:,1])
#用make_moons創建月亮型數據���,make_circles創建環形數據���,并將三組數據打包起來放在列表datasets中
moons=make_moons(noise=0.3, random_state=0)
circles=make_circles(noise=0.2, factor=0.5, random_state=1)
datasets = [moons,circles,linearly_separable]
figure = plt.figure(figsize=(6, 9))
i=1
#設置用來安排圖像顯示位置的全局變量i i = 1
#開始迭代數據��,對datasets中的數據進行for循環
for ds_index, ds in enumerate(datasets):
X, y = ds
# 對數據進行標準化處理
X = StandardScaler().fit_transform(X)
#劃分數據集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=42)
#定數據范圍����,以便后續進行畫圖背景的確定
#注意X[:,0]指橫坐標��,X[:�,1]指縱坐標
x1_min, x1_max = X[:, 0].min() - .5, X[:, 0].max() + .5
x2_min, x2_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#使畫板上每個點組成坐標的形式(沒間隔0.2取一個)�����,array1表示橫坐標����,array2表示縱坐標
array1,array2 = np.meshgrid(np.arange(x1_min, x1_max, 0.2), np.arange(x2_min, x2_max, 0.2))
# 顏色列表
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
########## 原始數據的現實 #########
# 用畫板上六個圖片位置(3����,2)的第i個
ax = plt.subplot(len(datasets), 2, i)
# 便簽添加
if ds_index == 0:
ax.set_title("Input data")
#畫出訓練數據集散點圖
ax.scatter(X_train[:, 0],#橫坐標
X_train[:, 1],#縱坐標
c=y_train,#意思是根據y_train標簽從cm_bright顏色列表中取出對應的顏色,也就是說相同的標簽有相同的顏色。
cmap = cm_bright, #顏色列表
edgecolors = 'k'#生成散點圖��,每一個點邊緣的顏色
)
#畫出測試數據集的散點圖�,其中比訓練集多出alpha = 0.4參數,以分辨訓練測試集
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test,cmap = cm_bright, alpha = 0.4, edgecolors = 'k')
#顯示的坐標范圍
ax.set_xlim(array1.min(), array1.max())
ax.set_ylim(array2.min(), array2.max())
#不顯示坐標值
ax.set_xticks(())
ax.set_yticks(())
#i+1顯示在下一個子圖版上畫圖
i += 1
####### 經過決策的數據顯示 #######
ax = plt.subplot(len(datasets), 2, i)
#實例化訓練模型
clf = DecisionTreeClassifier(max_depth=5).fit(X_train, y_train)
score = clf.score(X_test, y_test)
# np.c_是能夠將兩個數組組合起來的函數
# ravel()能夠將一個多維數組轉換成一維數組
#通過對畫板上每一個點的預測值確定分類結果范圍,并以此為依據通���,通過不同的顏色展現出來范圍
Z = clf.predict(np.c_[array1.ravel(), array2.ravel()])
Z = Z.reshape(array1.shape)
cm = plt.cm.RdBu # 自動選取顏色的實例化模型。
ax.contourf(array1#畫板橫坐標����。
, array2#畫板縱坐標
, Z# 畫板每個點對應的預測值m,并據此來確定底底板的顏色���。
, cmap=cm#顏顏色選取的模型����,由于Z的值只有兩個���,也可以寫出一個顏色列表���,指定相應顏色��,不讓其自動生成
, alpha=0.8
)
#和原始數據集一樣,畫出每個訓練集和測試集的散點圖
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, edgecolors = 'k')
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, edgecolors = 'k', alpha = 0.4)
ax.set_xlim(array1.min(), array1.max())
ax.set_ylim(array2.min(), array2.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_index == 0:
ax.set_title("Decision Tree")
#在右下角添加模型的分數
ax.text(array1.max() - .3, array2.min() + .3, ('{:.1f}%'.format(score * 100)),
size = 15, horizontalalignment = 'right')
i += 1
#自動調整子畫板與子畫板之間的的距離
plt.tight_layout()
plt.show()

從這里可以看出決策樹����,對于月亮型數據和二分類數據有比較好的分類效果���,但是對于環形的數據的分類效果就不是那么理想�����。
什么是隨機森林
隨機森林屬于集成算法,森林從字面理解就是由多顆決策樹構成的集合���,而且這些子樹都是經過充分生長的CART樹,隨機則表示構成多顆隨機樹是隨機生成的��,生成過程采用的是bossstrap抽樣法���,該算法有兩大優點��,一是運行速度快��,二是預測準確率高,被稱為最好用的算法之一�。
隨機森林的原理
該算法的核心思想就是采用多棵決策樹的投票機制��,完成分類或預測問題的解決。對于分類的問題�,將多個數的判斷結果用做投票���,根據根據少數服從多數的原則���,最終確定樣本所屬的類型�����,對于預測性的問題�����,將多棵樹的回歸結果進行平均�,最終確定樣本的預測。
將隨機森林的建模過程��,形象地描繪出來就是這樣:
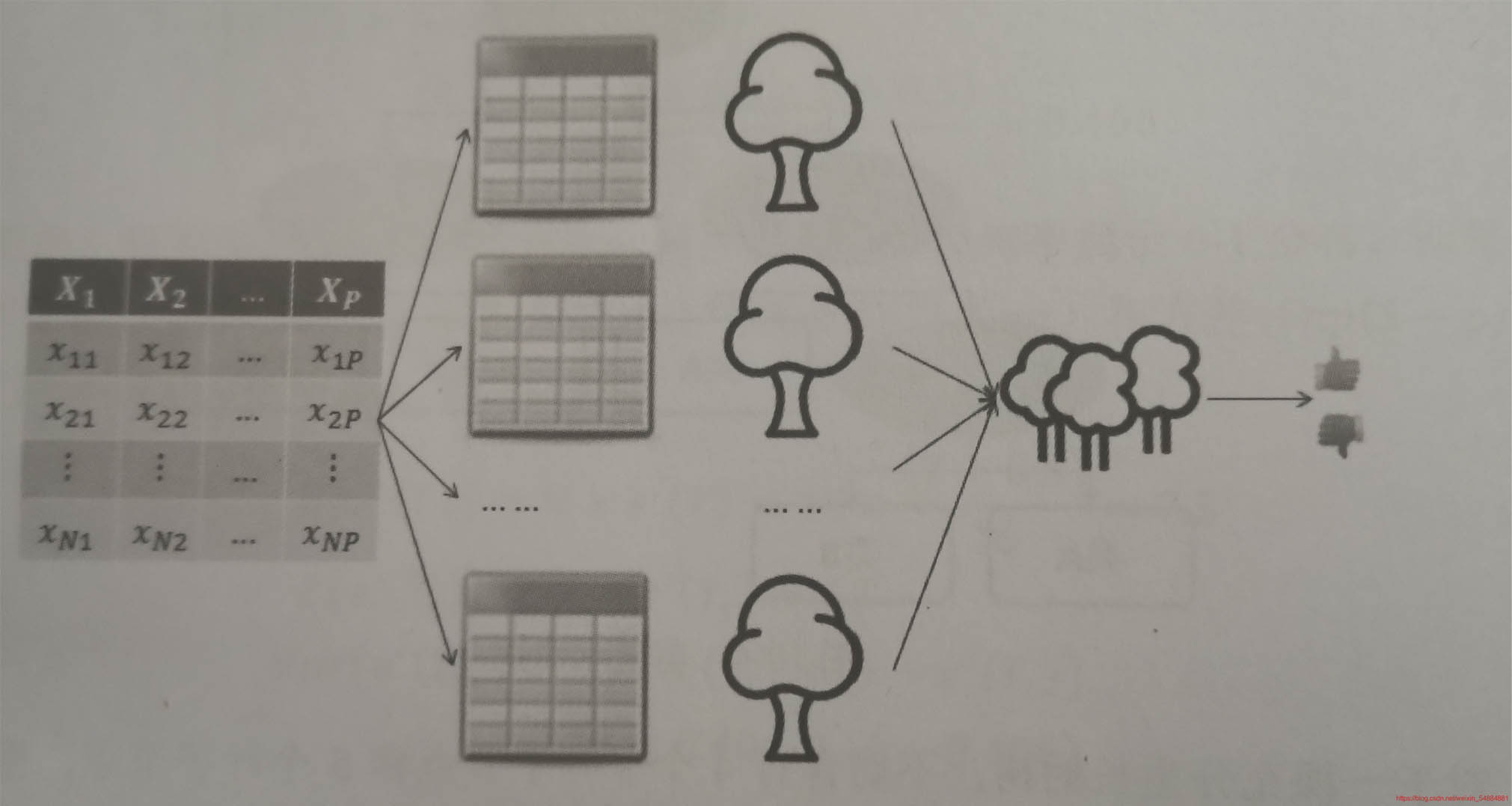
流程:
- 利用booststrap抽樣法�,從原始數據集中生成K個數據集,并且每一個數據集都含有N個觀測和P個自變量����。
- 針對每一個數據集構造一個CART決策樹���,在構造數的過程中����,并沒有將所有自變量用作節點字段的選擇而是隨機選擇P個字段(特征)
- 讓每一顆決策樹盡可能的充分生長���,使得樹中的每一個節點��,盡可能的純凈��,即隨機森林中的每一顆子樹都不需要剪枝。
- 針對K個CART樹的隨機森林,對于分類問題利用投票法將最高的的票的類別用于最后判斷結果�,對于回歸問題利用均值法�,將其作為預測樣本的最終結果�。
隨機森林常用參數
用分類的隨機森林舉例
RandomForestClassifier(n_estimators=10 # 用于對于指定隨機森林所包含的決策樹個數
,criterion="gini" # 用于每棵樹分類節點的分割字段的度量指標。和決策樹含義相同。
,max_depth=None # 用于每顆決策樹的最大深度����,默認不限制其生長深度���。
,min_samples_split=2 # 用于指定每顆決策數根節點或者中間節點能夠繼續分割的最小樣本量,默認2。
,min_samples_leaf=1 # 用于指定每個決策樹葉子節點的最小樣本量��,默認為1
,max_features="auto" # 用于指定每個決策樹包含的最多分割字段數(特征數)默認None��。表示分割時涉及使用所有特征
,bootstrap=True # #是否開啟帶外模式(有放回取值���,生成帶外數據)若不開啟�,需要自己劃分train和test數據集�����,默認True
,oob_score=False # #是否用帶外數據檢測 即是是否使用帶外樣本計算泛化��,誤差默認為false,袋外樣本是指每一個bootstrap抽樣時沒有被抽中的樣本
,random_state=None # 用于指定隨機數生成器的種子,默認None����,表示默認隨機生成器
,calss_weight # 用于因變量中類別的權重�����,默認每個類別權重相同
)
注:一般n_estimators越大,模型的效果往往越好��。但是相應的�����,任何模型都有決策邊界
n_estimators達到一定的程度之后��,隨機森林的精確性往往不在上升或開始波動
并且n_estimators越大,需要的計算量和內存也越大����,訓練的時間也會越來越長
隨機森林應用示例
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
wine=load_wine()
xtrain,xtest,ytrain,ytest=train_test_split(wine.data ,wine.target,test_size=0.3)
rfc=RandomForestClassifier(random_state=0
,n_estimators=10#生成樹的數量
,bootstrap=True
,oob_score=True#開啟袋外數據檢測
).fit(xtrain,ytrain)
rfc.score(xtest,ytest)
rfc.oob_score_#帶外數據作為檢測數據集
rfc.predict_proba(wine.data)#輸出所有數據在target上的概率
rfc.estimators_#所有樹情況
rfc.estimators_[1].random_state#某個樹random——state值
參數n_estimators對隨機森林的影響
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
wine=load_wine()
score=[]
for i in range(100):
rfc=RandomForestClassifier(random_state=0
,n_estimators=i+1
,bootstrap=True
,oob_score=False
)
once=cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
score.append(once)
plt.plot(range(1,101),score)
plt.xlabel("n_estimators")
plt.show()
print("best srore = ",max(score),"\nbest n_estimators = ",score.index(max(score))+1)
輸出:
best srore = 0.9833333333333334
best n_estimators = 12
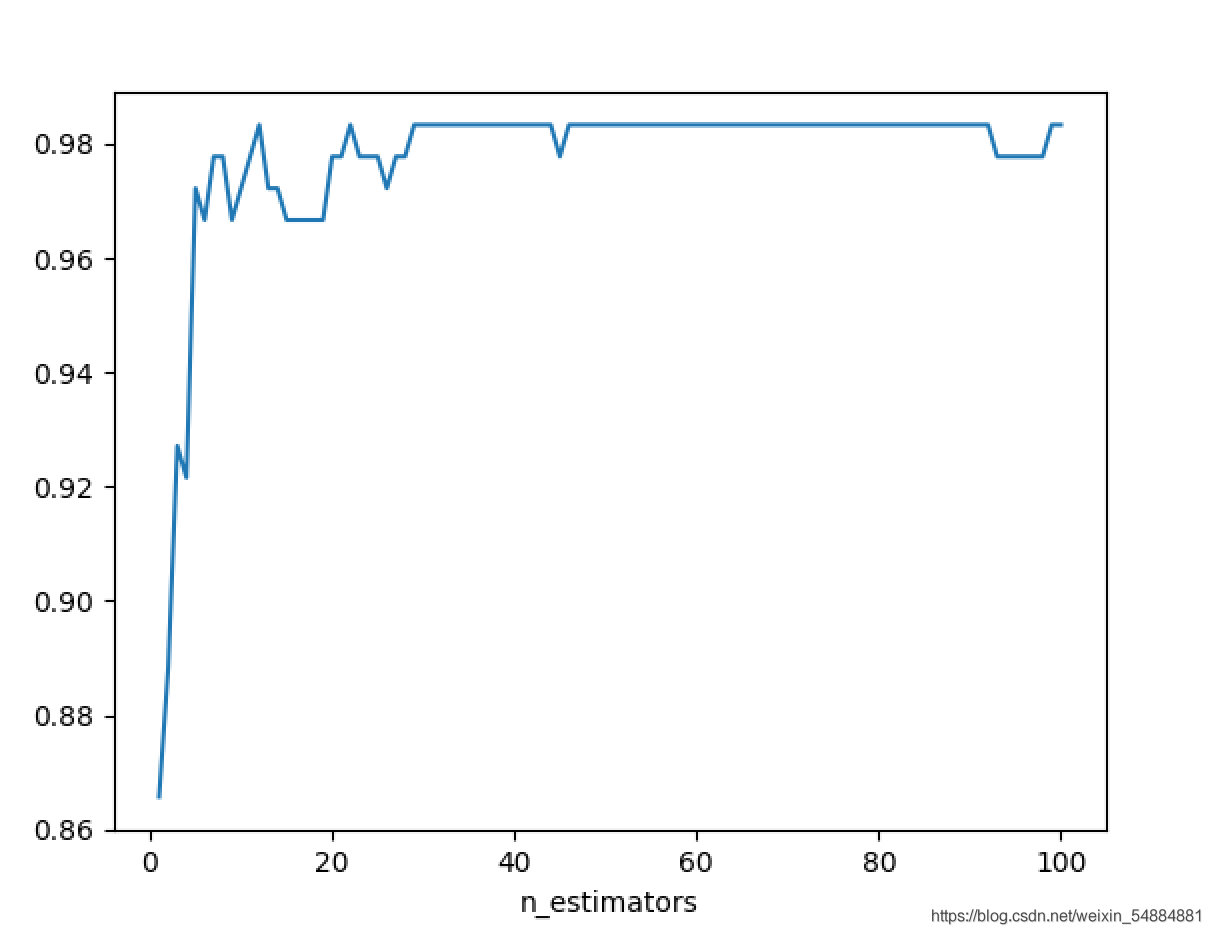
決策樹和隨機森林效果
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
wine=load_wine()
score1=[]
score2=[]
for i in range(10):
rfc=RandomForestClassifier(n_estimators=12)
once1=cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
score1.append(once1)
clf=DecisionTreeClassifier()
once2=cross_val_score(clf,wine.data,wine.target,cv=10).mean()
score2.append(once2)
plt.plot(range(1,11),score1,label="Forest")
plt.plot(range(1,11),score2,label="singe tree")
plt.legend()
plt.show()
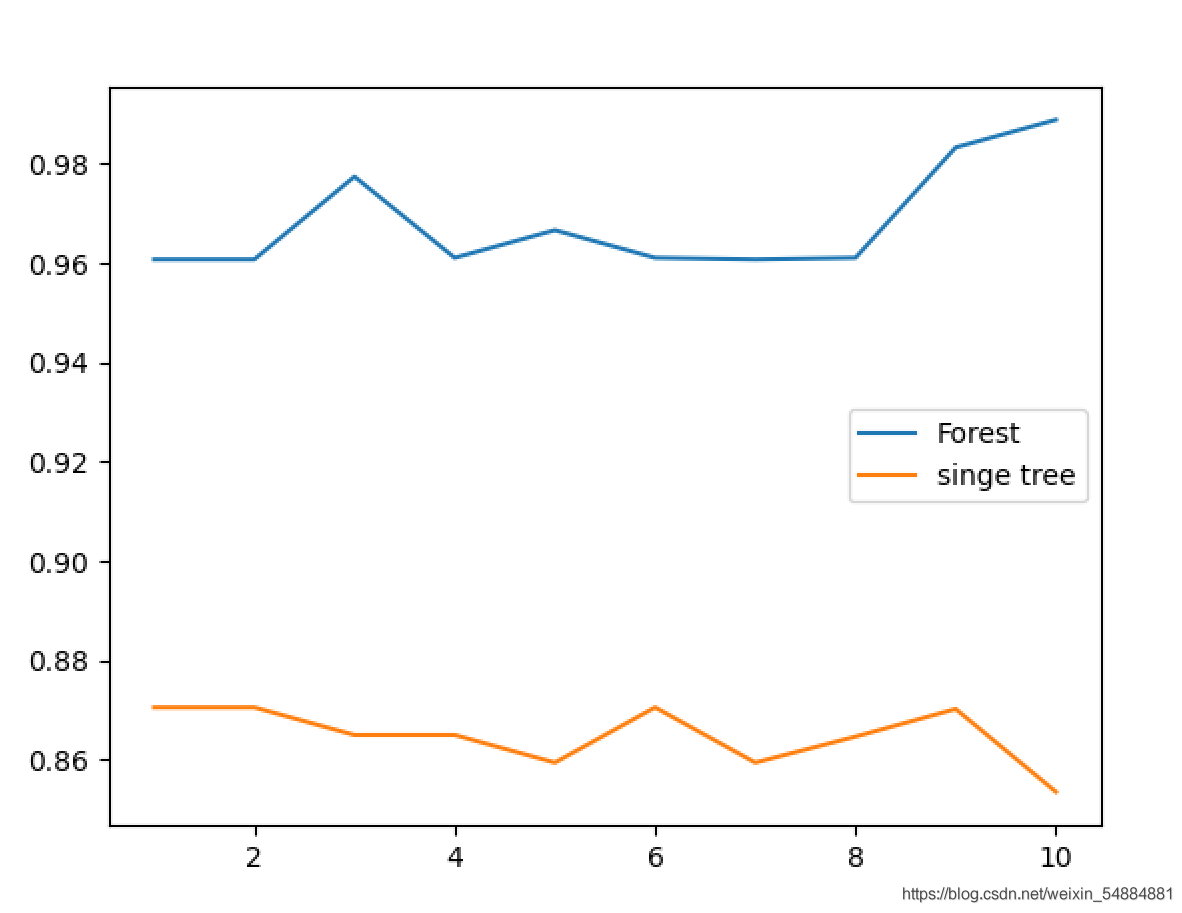
從圖像中可以直觀的看出:多個決策樹組成的隨機森林集成算法的模型效果要明顯優于單個決策樹的效果。
實例用隨機森林對乳腺癌數據的調參
n_estimators
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
cancer = load_breast_cancer()
scores=[]
for i in range(1,201,10):
rfc = RandomForestClassifier(n_estimators=i, random_state=0).fit(cancer.data,cancer.target)
score = cross_val_score(rfc,cancer.data,cancer.target,cv=10).mean()
scores.append(score)
print(max(scores),(scores.index(max(scores))*10)+1)
plt.figure(figsize=[20,5])
plt.plot(range(1,201,10),scores)
plt.show()
0.9649122807017545 111
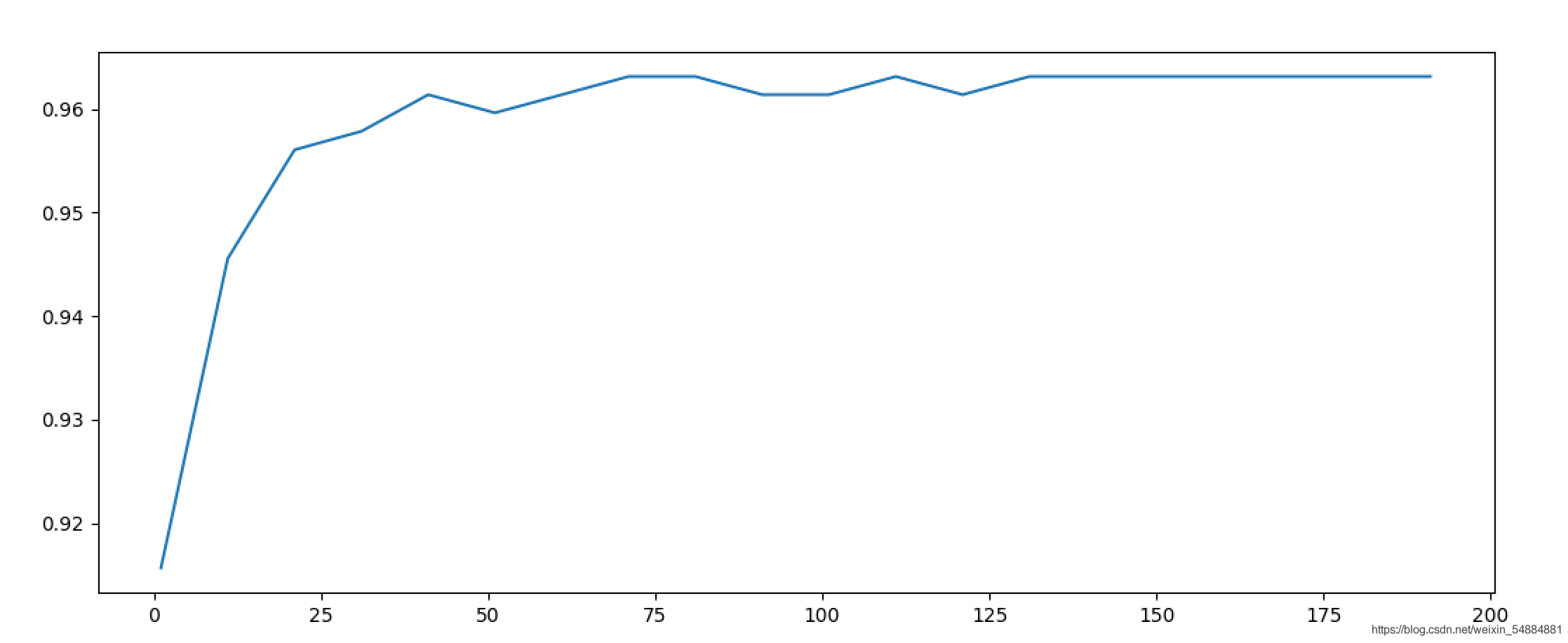
max_depth
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
cancer = load_breast_cancer()
scores=[]
for i in range(1,20,2):
rfc = RandomForestClassifier(n_estimators=111,max_depth=i, random_state=0)
score = cross_val_score(rfc,cancer.data,cancer.target,cv=10).mean()
scores.append(score)
print(max(scores),(scores.index(max(scores))*2)+1)
plt.figure(figsize=[20,5])
plt.plot(range(1,20,2),scores)
plt.show()
0.9649122807017545 11
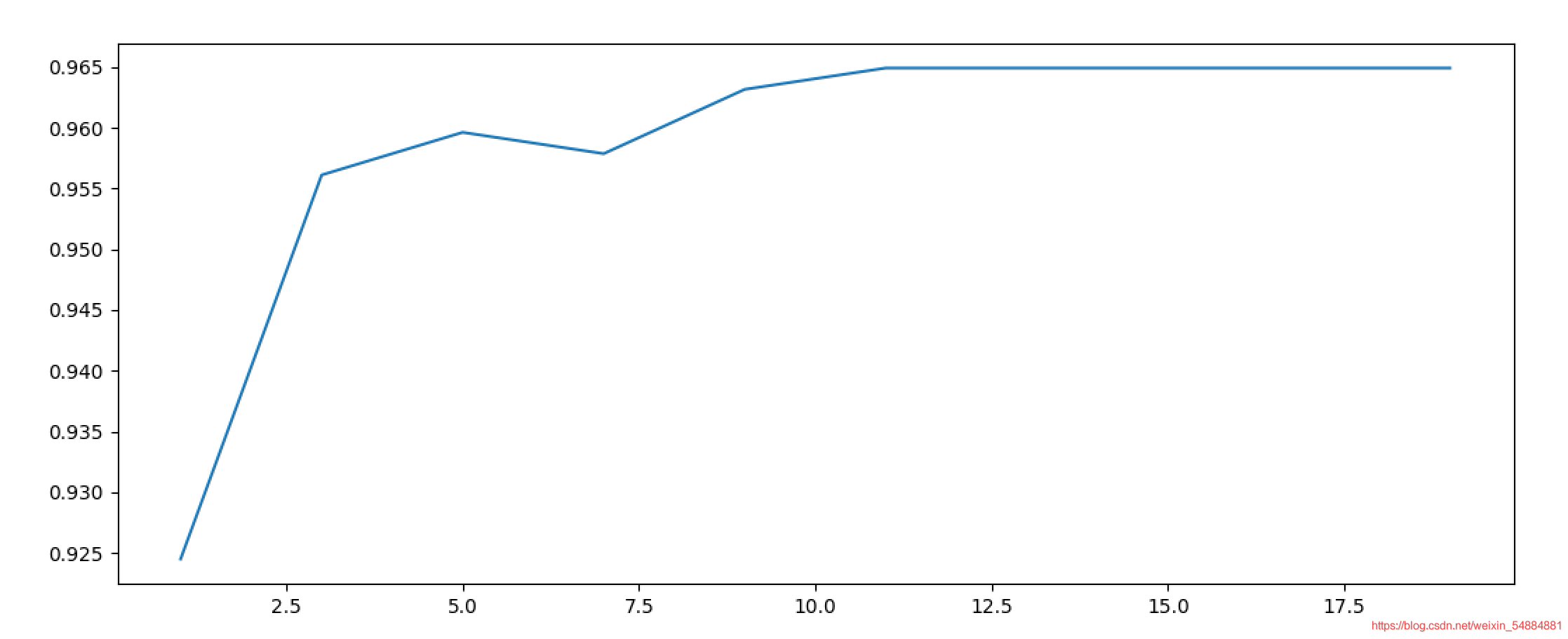
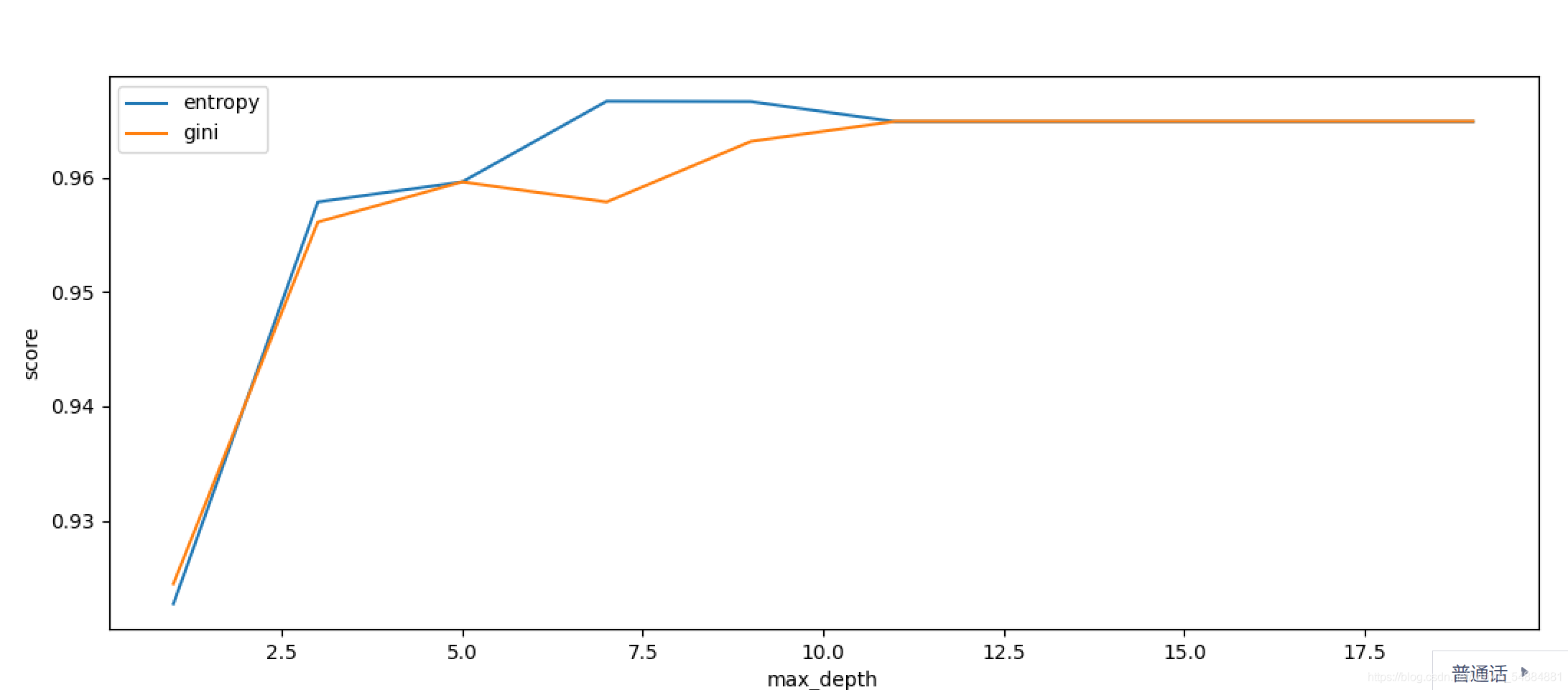
gini改為entropy
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
cancer = load_breast_cancer()
scores=[]
for i in range(1,20,2):
rfc = RandomForestClassifier(n_estimators=111,criterion="entropy",max_depth=i, random_state=0)
score = cross_val_score(rfc,cancer.data,cancer.target,cv=10).mean()
scores.append(score)
print(max(scores),(scores.index(max(scores))*2)+1)
plt.figure(figsize=[20,5])
plt.plot(range(1,20,2),scores)
plt.show()
0.9666666666666666 7
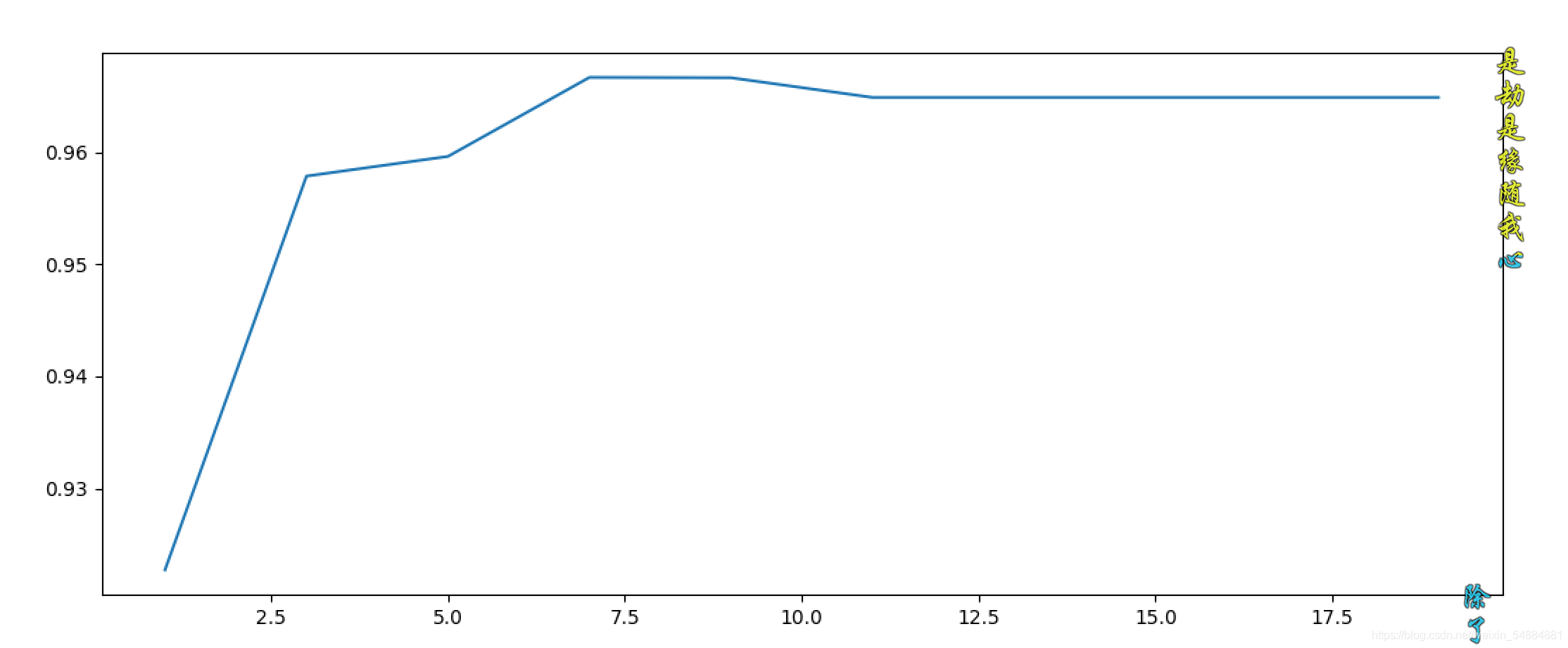
gini和entropy結果圖片:
到此這篇關于Python機器學習之決策樹和隨機森林的文章就介紹到這了,更多相關Python 決策樹和隨機森林內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家�����!
您可能感興趣的文章:- python實現決策樹�、隨機森林的簡單原理
- Python決策樹和隨機森林算法實例詳解