目錄
- 一、圓周率的歷史
- 二、用python計算圓周率π
- 【方法】
- 【程序設計思路】
- 【軟件環境】
- 【代碼】
- 【結果展示】
- 【常見問題答疑】
一、圓周率的歷史
1、中國
魏晉時期,劉徽曾用使正多邊形的邊數逐漸增加去逼近圓周的方法 (即「割圓術」),求得π的近似值3.1416。
漢朝時,張衡得出π的平方除以16等于5/8,即π等于10的開方(約為3.162)。雖然這個值不太準確,但它簡單易理解,所以也在亞洲風行了一陣。
王蕃(229-267)發現了另一個圓周率值,這就是3.156, 但沒有人知道他是如何求出來的(ps. 沒開源唄!)。
公元5世紀,祖沖之和他的兒子以正24576邊形,求出圓周率約為355/113,和真正的值相比,誤差小于八億分之一。
這個紀錄在一千年后才給打破。(ps. 在大部分人不知股股定理年代,真牛!)
2、印度
約在公元530年,數學大師阿耶波多利用384邊形的周長,算出圓周率約為√9.8684。
婆羅門笈多采用另一套方法,推論出圓周率等于10的平方根。(ps. 跟張衡大佬的結果一致,但過程不同)
3、歐洲
斐波那契算出圓周率約為3.1418。
韋達用阿基米德的方法,算出3.1415926535π3.1415926537。
他是第一個以無限乘積敘述圓周率的人。
魯道夫萬科倫以邊數多過32000000000的多邊形算出有35個小數位的圓周率。
華理斯在1655年求出一道公式π/2=2×2×4×4×6×6×8×8...../3×3×5×5×7×7×9×9......
歐拉發現的e的iπ次方加1等于0,成為證明π是超越數的重要依據。
二、用python計算圓周率π
【方法】
蒙特卡洛法
【程序設計思路】
使用python random庫隨機生成點,落在正方形內,計算正方形內的圓內落點與正方形內落點之比,近似為面積之比,隨機數越隨機,數量越大越準確。
【軟件環境】
python 3.6(本程序可兼容python 2.x)
【代碼】
from random import random
from time import perf_counter
def calPI(N = 100):
hits = 0
start = perf_counter()
for i in range(1, N*N+1):
x, y = random(), random()
dist = pow(x ** 2 + y ** 2, 0.5)
if dist = 1.0:
hits += 1
pi = (hits * 4) / (N * N)
use_time = perf_counter() - start
return pi, use_time
PI, use_time = calPI(10000)
print('use Monte Carlo method to calculate PI: {}'.format(PI))
print('use time: {} s'.format(use_time))
【結果展示】
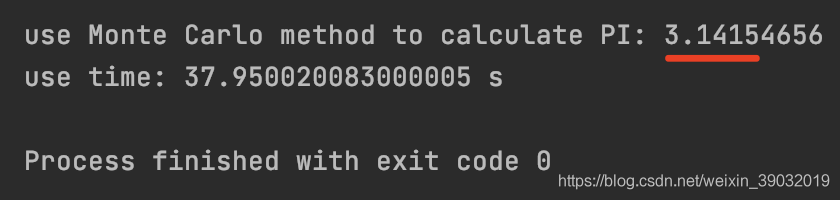
震驚:10000次隨機數,精確到3.1415了,把橋哥放在1000年前,可不得了
【常見問題答疑】
(每篇文章都有很多粉絲私信我,提前答疑一下!!):
1、運行程序前,先導入頂部的包,怎么導包看這里:https://www.jb51.net/article/221337.htm
2、本文使用的random 和 time庫為python自帶,無需導入,可直接執行程序。
以上就是實現用python算法計算圓周率的小訣竅的詳細內容,更多關于python算法計算圓周率的資料請關注腳本之家其它相關文章!
您可能感興趣的文章:- Python編程實現蟻群算法詳解
- python二叉樹常用算法總結
- Python代碼實現粒子群算法圖文詳解
- python列表與列表算法詳解(2)
- python列表與列表算法詳解
- Python 蟻群算法詳解