中国女人特级毛片,97久久久久

主頁 > 知識庫 > C語言實現二叉搜索樹的完整總結

C語言實現二叉搜索樹的完整總結

1、二叉樹的構建

我們都知道二叉搜索樹的特點是：當前節點的值大于它的左子樹的值，小于等于右子樹的值。所以我們這里可以通過迭代的方式構建二叉搜索樹，當然也可以通過遞歸的方式構建二叉樹。

定義一個結構體，表示節點:

typedef struct NODE{
    int va;
    struct NODE *left,*right;
}Node;

①通過迭代的方式實現二叉搜索樹的構建,值得注意的是，這種方式構建二叉搜索樹的時候,需要定義一個變量，表示這個節點插入的位置是父節點的左子節點還是右子節點的位置，同時定義一個變量，表示插入的父節點。

Node * createBinaryTree(Node *root,int val){
    int isLeftChild = 0;//定義一個臨時變量，表示這個新節點的插入位置是否為它的左子節點
    Node *cur = root,*parent = NULL,*node;
    node = (Node *)malloc(sizeof(Node));
    if(node == NULL){
       printf("創建節點失敗!!!\n");
       exit(0);//退出虛擬機
    }
    node->val = val;
    node->left = node->right = NULL;
    while(*cur != NULL){
     //找到新節點要插入的位置
       parent = cur;
       if(cur->val > x){
          cur = cur->left;//新節點的值小于當前節點的值，那么就往當前節點的左子樹方向進行查找
          isLeftChild = 1;
      } else{
          cur = cur->right;//如果新節點的值大于等于當前節點的值，那么就往當前節點的右子樹方向進行查找
          isLeftChild = 0;
      }
    }
   //判斷parent/root是否為空，如果為空，說明新節點是根節點
   if(pre == NULL){
     root = node;
   }else{
     //parent不為空，說明不是空樹，這是需要判斷插入的位置是否是在左子節點的位置
     if(isLeftChild){
         parent->left = node;
     }else{
         parent->right= node;
      }
   }
   return root;
}

②通過迭代的方式進行創建二叉搜索樹

Node *createBinaryTree(Node *root,int val){
     if(root == NULL){
          root = (Node *)malloc(sizeof(Node));//給新節點分配空間
          if(root == NULL){
             printf("創建節點失敗!!!\n"):
             exit(0);//退出虛擬機
          }
          root->val = val;
          root->left = root->right = NULL;
      }else{
      //如果當前的節點不為空，那么就判斷新節點插入的是左子節點還是右子節點的位置
         if(val  root->val)//新節點的值小于當前節點的值，說明將其插入在當前節點左子樹的位置
            root->left = createBinaryTree(root->left,val);
         else//新節點的值大于等于當前節點的值，說明時將其插入在當前節點的右子樹位置
            root->right = createBinaryTree(root->right,val);
      }
      return root;
}

2、二叉樹的遍歷

二叉樹的遍歷主要包括幾種遍歷方式，分別是前序遍歷，中序遍歷，后序遍歷，層序遍歷。
前序遍歷：先訪問當前的節點，然后訪問它的左子樹，最后訪問它的右子樹。
中序遍歷：先訪問當前節點的左子樹，然后訪問自身，最后訪問它的右子樹。
后序遍歷：先訪問當前節點的左子樹，然后訪問當前節點的右子樹，最后才訪問自身。
層序遍歷：一層一層，從左到右遍歷的。

前序遍歷

遞歸實現

void preOrderDisplay(Node *root){
   if(root != NULL){
       printf("%5d",root->val);//訪問自身
       preOrderDisplay(root->left);//訪問當前節點的左子樹
       preOrderDisplay(root->right);//訪問當前節點的右子樹
   }
}

迭代實現

注意的是，通過迭代實現二叉樹的前序遍歷，我們需要利用到棧。

void preOrderTraversal(Node *root){
  Stack *s;
  if(!createStack(s)){
    printf("創建棧失敗!!!\n");
    return;
  }
  Node *t = root,k;
  while(t != NULL || !isEmpty(s)){
    //當前的節點不為空，或者棧不為空，那么就繼續進循環
    while(t!= NULL){
        //如果當前的節點不為空，那么就將當前的節點輸出，然后將它的左子樹壓入棧中（遍歷到最左）
        printf("%5d",t->val);//由于是前序遍歷，那么先輸出父節點的值
        pushStack(s,t);
        t = t->left;
    }
    if(!isEmpty(s)){
        //如果棧不為空，那么這時候，將從棧中跳出一個節點，并且將獲得它的右子樹，然后將右子樹壓入棧中
        popStack(s,k);//（跳出一個節點）
        t = k.right;//將右子樹重復上面的操作（往這個跳出節點k的右子樹方向移動)
    }
  }
}

中序遍歷

遞歸實現

//利用遞歸中序遍歷樹
void InOrderDisplay(Node *root){
   if(root != NULL){
    //如果節點不為空，那么遞歸實現中序遍歷
       InOrderDisplay(root->left);//先訪問左子樹
       printf("%5d",root->val);//訪問自身
       InOrderDisplay(root->right);//訪問右子樹
   }
}

迭代實現

/*
利用迭代循環實現樹的中序遍歷
基本思路：利用堆棧實現的
基本步驟:
1、判斷當前的節點或者棧是否為空，如果其中至少有一個不為空，那么
這時候將進入循環
2、判斷當前的節點是否為空，（必須要判斷，因為進入外部循環的循環條件有兩個，所以不知道是否因為當前
節點是否為空），如果節點不為空，那么將當前的節點壓入棧中，然后當前的節點變成它的左節點，將它的左子樹壓入
棧中
3、判斷棧是否為空，將棧頂節點跳出，并將其輸出，然后后去這個跳出節點的右子節點

*/
void InOrderTraversal(Node *root){
   Stack *s;
   Node *t = root,k;
   if(!createStack(s)){
      printf("創建棧失敗!!!\n");
      return;
   }
   while(t != NULL || !isEmpty(s)){
      while(t != NULL){
         pushStack(s,t);//將當前的節點及其左子樹壓入棧中（遍歷到最左）
         t = t->left;
      }
      if(!isEmpty(s)){
        //從棧中跳出最后一個左子節點的父節點
        popStack(s,k);
        printf("%5d",k.val);//輸入當前節點的值
        t = k.right;//將其右子樹壓入棧中（往跳出節點k的右子樹方向移動)
      }
   }
}

后序遍歷

遞歸實現

/*
遞歸實現樹的后序遍歷
*/
void postOrderDisplay(Node *root){
    if(root != NULL){
        //當前的節點不為空，那么就先訪問左子樹，然后訪問右子樹，最后訪問當前的節點
        postOrderDisplay(root->left);
        postOrderDisplay(root->right);
        printf("%5d",root->val);
    }
}

迭代實現

/*
利用迭代實現樹的后序遍歷:
基本思路:
1、判斷當前的節點或者棧是否為空，如果其中至少有一個不為空，那么循環繼續
2、判斷該當前的節點是否為空，如果不為空，那么就將當前的節點及其左子樹壓入棧中
3、判斷當前的棧是否為空，如果不為空，那么就從棧中跳出一個節點
獲取這個節點的右子節點，如果這個右子節點為空，那么就將當前的節點輸出，然后再吃從棧中跳出一個節點
4、重復上面的2、3步驟
*/
void postOrderTraversal(Node *root){
   Node *t = root,k,pre;//pre表示上一次訪問過的右子節點
   Stack *s;
   if(!createStack(s)){
    printf("創建棧失敗!!!\n");
    return;
   }
   while(t != NULL || !isEmpty(s)){
    //如果當前的節點不為空或者棧不為空，那么就繼續循環遍歷
     while(t != NULL){
        //如果當前的節點不為空，那么就將其壓入棧中
        pushStack(s,t);
        t = t->left;
     }
     //注意這里并不是直接從棧中跳出一個節點,而是先獲取棧頂節點，判斷條件滿足之后才跳出節點
     if( getTop(s,k)  k.right == NULL || pre.val == k.right->val){
       /*
       判斷當前的棧頂節點的右子節點是否為空，或者這個棧頂的右子節點已經輸
       出過了，如果這個棧頂節點的右子節點為空或者已經輸出過了，那么就將這
       個棧頂節點從棧中跳出，并輸出它的值否則，就將這個棧頂節點的右子樹壓
       入棧中,重復循環操作
       */
        popStack(s,k);
        pre = k;
        printf("%5d",k.val);
     }else{
        t = k.right;//如果上面的條件不滿足，那么就往它的右子樹方向移動
     }
   }
}

測試完整代碼:

#includestdio.h>
#includestdlib.h>
#define MAX_SIZE 100
#define INCREMENT 10
#define ERROR 0
#define OK 1
typedef struct NODE{
    int val;
    struct NODE *left;
    struct NODE *right;
}Node;
typedef struct STACK{
    Node * arr;
    int top;
}Stack;
//創建棧
int createStack(Stack *s){
    s->arr = (Node *)malloc(sizeof(Node) * MAX_SIZE);//分配MAX_SIZE個空間
    if(s->arr == NULL)
        //如果arr為空，說明分配空間事變，這時候返回ERROR
        return ERROR;
    s->top = 0;
    return OK;
}
//壓棧
int pushStack(Stack *s,Node *node){
    if(s->top == MAX_SIZE){
        return ERROR;
    }
    Node t;
    t.val = node->val;
    t.left = node->left;
    t.right = node->right;
    s->arr[s->top++] = t;
    return OK;
}
//出棧
int popStack(Stack *s,Node node){
    if(s->top == 0){
        //如果棧為空，那么這時候返回ERROR
        return ERROR;
    }
    node = s->arr[--s->top];//獲取棧頂節點
    return OK;
}
int getTop(Stack *s,Node k){
    if(s->top == 0)
        return ERROR;
    k = s->arr[s->top - 1];
    return OK;
}
//判斷棧是否為空
int isEmpty(Stack *s){
    return s->top == 0;
}
/*
節點的插入基本思路:
判斷這顆樹是否為空樹，如果是一棵空樹，那么新節點就是整棵樹的
根節點，如果不是，那么就需要通過遍歷找到插入的位置。
根據二叉搜索樹的特點，如果新節點的值小于根節點或者父節點的值，那么就
往左邊走，找到第一個為空的地方，然后將其插入；如果新節點的值大于等于父節點的值，
那么就往右邊走，找到第一個為空的地方，將其插入。
值得注意的是，我們需要標記插入的是否為左子節點還是右子節點，所以需要定義一個臨時
變量，判斷插入的位置是否為父節點的左節點
*/
Node * insert(Node *root,int val){
   Node *node = (Node *)malloc(sizeof(Node));
   node->val = val;
   node->left = NULL;
   node->right = NULL;
  //如果不是空樹，那么就需要定義臨時變量，表示插入的位置是否為左節點
  //同時定義一個臨時節點，表示要插入位置的父節點
  Node *current = root,*parent = NULL;
  int isLeftChild = 1; //值為1表示插入的是父節點的左子節點的位置，否則為右子節點的位置
  while(current != NULL){
     parent = current;//表示插入位置的父節點
     if(current->val > val){
        //如果當前的節點比新節點的值大，那么就往左子節點的方向走
        isLeftChild = 1;
        current = current->left;
     }else{
        isLeftChild = 0;
        current = current->right;
     }
  }
  if(parent == NULL){
    //如果parent為空，說明是一棵空樹，此時新節點就是根節點
    root = node;
  }else{
    if(isLeftChild)
        parent->left = node;
    else
        parent->right = node;
  }
  return root;
}
//利用遞歸中序遍歷樹
void InOrderDisplay(Node *root){
   if(root != NULL){
    //如果節點不為空，那么遞歸實現中序遍歷
       InOrderDisplay(root->left);//先訪問左子樹
       printf("%5d",root->val);//訪問自身
       InOrderDisplay(root->right);//訪問右子樹
   }
}
void preOrderDisplay(Node *root){
   if(root != NULL){
    //如果root節點不為空，那么就進行遞歸
      printf("%5d",root->val);
      preOrderDisplay(root->left);//訪問左子樹
      preOrderDisplay(root->right);//訪問右子樹
   }
}
/*
遞歸實現樹的后序遍歷
*/
void postOrderDisplay(Node *root){
    if(root != NULL){
        //當前的節點不為空，那么就先訪問左子樹，然后訪問右子樹，最后訪問當前的節點
        postOrderDisplay(root->left);
        postOrderDisplay(root->right);
        printf("%5d",root->val);
    }
}
/*
利用迭代實現樹的后序遍歷:
基本思路:
1、判斷當前的節點或者棧是否為空，如果其中至少有一個不為空，那么循環繼續
2、判斷該當前的節點是否為空，如果不為空，那么就將當前的節點及其左子樹壓入棧中
3、判斷當前的棧是否為空，如果不為空，那么就從棧中跳出一個節點
獲取這個節點的右子節點，如果這個右子節點為空，那么就將當前的節點輸出，然后再吃從棧中跳出一個節點
4、重復上面的2、3步驟
*/
void postOrderTraversal(Node *root){
   Node *t = root,k,pre;//pre表示上一次訪問過的右子節點
   Stack *s;
   if(!createStack(s)){
    printf("創建棧失敗!!!\n");
    return;
   }
   while(t != NULL || !isEmpty(s)){
    //如果當前的節點不為空或者棧不為空，那么就繼續循環遍歷
     while(t != NULL){
        //如果當前的節點不為空，那么就將其壓入棧中
        pushStack(s,t);
        t = t->left;
     }
     //注意這里并不是從棧中跳出一個節點
     if( getTop(s,k)  k.right == NULL || pre.val == k.right->val){
       /*
       判斷當前的棧頂節點的右子節點是否為空，或者這個棧頂的右子節點已經輸出過了
       如果這個棧頂節點的右子節點為空或者已經輸出過了，那么就將這個棧頂節點從棧中跳出，并輸出它的值
       否則，就將這個棧頂節點的右子樹壓入棧中,重復循環操作
       */
        popStack(s,k);
        pre = k;
        printf("%5d",k.val);
     }else{

        t = k.right;
     }
   }
}
/*
利用迭代循環實現樹的中序遍歷
基本思路：利用堆棧實現的
基本步驟:
1、判斷當前的節點或者棧是否為空，如果其中至少有一個不為空，那么
這時候將進入循環
2、判斷當前的節點是否為空，（必須要判斷，因為進入外部循環的循環條件有兩個，所以不知道是否因為當前
節點是否為空），如果節點不為空，那么將當前的節點壓入棧中，然后當前的節點變成它的左節點，將它的左子樹壓入
棧中
3、判斷棧是否為空，將棧頂節點跳出，并將其輸出，然后后去這個跳出節點的右子節點

*/
void InOrderTraversal(Node *root){
   Stack *s;
   Node *t = root,k;
   if(!createStack(s)){
      printf("創建棧失敗!!!\n");
      return;
   }
   while(t != NULL || !isEmpty(s)){
      while(t != NULL){
         pushStack(s,t);//將當前的節點及其左子樹壓入棧中
         t = t->left;
      }
      if(!isEmpty(s)){
        //從棧中跳出最后一個左子節點的父節點
        popStack(s,k);
        printf("%5d",k.val);
        t = k.right;//將其右子數壓入棧中
      }

   }
}
/*
前序遍歷的非遞歸實現:
基本思路：利用棧實現的
1、如果當前節點不為空或者當前棧不為空，那么就進入循環語句
2、如果當前的節點不為空，那么這時候將當前的節點輸出，然后將當前節點壓入棧中
然后這個節點往它的左子節點的方向移動，重復2的步驟，知道左子節點為空
3、如果棧不為空，那么就從棧中跳出一個節點，然后將往這個節點的右子樹方向移動
4、重復上面的2、3步驟
*/
void preOrderTraversal(Node *root){
  Stack *s;
  if(!createStack(s)){
    printf("創建棧失敗!!!\n");
    return;
  }
  Node *t = root,k;
  while(t != NULL || !isEmpty(s)){
    //當前的節點不為空，或者棧不為空，那么就繼續進循環
    while(t!= NULL){
        //如果當前的節點不為空，那么就將當前的節點輸出，然后將它的左子樹壓入棧中
        printf("%5d",t->val);//由于是前序遍歷，那么先輸出父節點的值
        pushStack(s,t);
        t = t->left;
    }
    if(!isEmpty(s)){
        //如果棧不為空，那么這時候，將從棧中跳出一個節點，并且將獲得它的右子樹，然后將右子樹壓入棧中
        popStack(s,k);
        t = k.right;//將右子樹重復上面的操作
    }
  }
}
int main(){
  int n,i,val;
  Node *root = NULL;
  printf("請輸入樹的節點個數:");
  scanf("%d",n);
  printf("請輸入各個節點的值:");
  for(i = 0; i  n; i++){
    scanf("%d",val);
    root = insert(root,val);
  }
  printf("遞歸實現樹的中序遍歷:");
  InOrderDisplay(root);
  printf("\n");
  printf("迭代實現數的中序遍歷:");
  InOrderTraversal(root);
  printf("\n");
  printf("遞歸實現樹的前序遍歷:");
  preOrderDisplay(root);
  printf("\n");
  printf("迭代實現樹的前序遍歷:");
  preOrderTraversal(root);
  printf("\n");
  printf("遞歸實現樹的后序遍歷:");
  postOrderDisplay(root);
  printf("\n");
  printf("迭代實現樹的后序遍歷:");
  postOrderTraversal(root);
  printf("\n");
  return 0;
}

運行結果:

層序遍歷

二叉搜索樹的層序遍歷，需要使用到隊列。
基本思路：
1·、定義一個隊列
2、創建二叉搜索樹
3、將當前的根節點壓入到隊列中
4、當隊列不為空的時候，那么我們將從隊列中跳出節點，將它的值輸出，然后判斷它的左右子節點是否為空，如果不為空，那么我們就將他們壓入到隊列中
5、重復4的操作，直到隊列為空，此時層序遍歷完成。
代碼實現:

/*
實現二叉樹的層序遍歷基本思路：
利用隊列來實現的
1、判斷當前的節點是否為空或者隊列是否為空，如果
不為空，那么就將當前的節點壓入隊列，同時需要判斷當前
節點的子節點是否為空，如果不為空，那么同樣的將它的子節點壓入隊列中
2、如果把這個節點的子節點壓入道隊列之后，那么這時候我們需要將從
隊列中跳出一個節點，然后將這個節點的信息輸出。
3、獲取隊列頭，如果隊列頭不為空，那么這時候重復2的操作
*/
#includestdio.h>
#includestdlib.h>
#define MAX_SIZE 100
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;
struct NODE{
   int val;
   Node left;
   Node right;
};
typedef struct QUEUE{
   List arr;
   int front;//隊頭指針
   int rear;//隊尾指針
}Queue;
int init(Queue s){
  s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定義一個指針類型的數組
  if(s.arr == NULL){
    return ERROR;
  }

  int i;
  //給數組初始化之后還沒有可以，還需要給所有的節點分配空間，如果沒有這一步，那么就會發生報錯
  for(i = 0; i  MAX_SIZE; i++){
    s.arr[i] = (Node)malloc(sizeof(struct NODE));
    if(s.arr[i] == NULL)
        return ERROR;
  }
  s.front = s.rear = 0;//將隊頭指針、隊尾指針都初始為0
  return OK;
}
//壓入隊列
int pushQueue(Queue s,Node node){
   if((s.rear + 1) % MAX_SIZE == s.front){
    //如果棧滿了，返回ERROR
    printf("隊列為滿!!!\n");
    return ERROR;
   }
   s.arr[s.rear] = node;
   s.rear = (s.rear + 1) % MAX_SIZE;
   return OK;
}
int popQueue(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   s.front = (s.front + 1) % MAX_SIZE;
   return OK;
}
int getTop(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   return OK;
}
int isEmpty(Queue s){
   return s.rear == s.front;//判斷隊列是否為空
}
int getSize(Queue s){
   return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//獲取隊列的個數
}
/*
利用遞歸創建二叉查找樹
基本思路:
1、首先判斷當前的節點是否為空，如果為空，就說明這個位置是新節點要插入的位
置此時需要給新節點分配空間，判斷創建節點是否成功，如果失敗，那么輸出錯誤信
息，否則將這個節點返回
2、如果當前的節點不為空，那么這時候拿當前節點和新節點的值進行比較，如果
新節點的值大于等于當前的節點，那么意味著新節點會插入在當前節點的右子樹位
置，否則插入在當前節點的左子樹位置
*/
Node createBinaryTree(Node root,int x){
   if(root == NULL){
      Node node = (Node)malloc(sizeof(struct NODE));
      if(node == NULL){
        //printf("創建新節點失敗!!!\n");
        exit(0);
      }
      node->val = x;
      node->left = NULL;
      node->right = NULL;
      root = node;
   }else{
      //如果當前的節點不為空，說明不是要插入的位置，需要和當前節點的值進行
      //比較，如果大于等于當前節點的值，那么往右子樹的方向進行遞歸，否則往左子樹方向遞歸
      if(x  root->val){
        root->left = createBinaryTree(root->left,x);
      }else{
        root->right = createBinaryTree(root->right,x);
      }
   }
   return root;
}
/*
利用遞歸實現樹的后序遍歷
*/
void postOrderTraversal(Node root){
   if(root != NULL){
    //如果當前的節點不為空，那么就先訪問左子樹，然后訪問右子樹，最后訪問自身
      postOrderTraversal(root->left);
      postOrderTraversal(root->right);
      printf("%5d",root->val);
   }
}

/*
利用遞歸實現樹的前序遍歷
*/
void preOrderTraversal(Node root){
   if(root != NULL){
      printf("%5d",root->val);
      preOrderTraversal(root->left);
      preOrderTraversal(root->right);
   }
}
/*
利用隊列實現樹的層序遍歷
*/
void levelOrderTraversal(Node root){
     Node t = root,k;
     Queue q;
     init(q);
     pushQueue(q,t);//將根節點壓入隊列中
     while(!isEmpty(q)){
        //如果隊列不為空，那么就繼續進行循環 
        popQueue(q,t);//將從隊列中跳出一個節點，然后將這個節點的信息輸出
        printf("%5d",t->val);
        /*
        判斷從隊列中跳出的節點是否含有左右子節點，如果含有，那么就將這個節
        點的左右子節點壓入到隊列中
        */
        if(t->left != NULL){
            pushQueue(q,t->left);
        }
        if(t->right != NULL){
            pushQueue(q,t->right);
        }
     }
}
/*
為了使層序遍歷看的更加直觀，我們將定義一個臨時變量size，表示在壓入隊列之前
隊列的元素個數，然后將隊列中的元素不斷跳出，并且輸出對應的信息，與此同時，
每跳出一個節點，我們都需要判斷這個節點是否含有左右子節點，如果含有，那么就
將它的子節點壓入到隊列中去
*/
void levelOrderTraversal2(Node root){
     Node t = root,k;
     Queue q;
     int size,i;
     init(q);
     pushQueue(q,t);//將根節點壓入隊列中
     while(!isEmpty(q)){
        size = getSize(q);
        for(i = 1; i = size; i++){
            popQueue(q,k);
            printf("%5d",k->val);
            //每跳出一個節點，那么就將它的左右子節點壓入到隊列中
            if(k->left != NULL){
                pushQueue(q,k->left);
            }
            if(k->right != NULL){
                pushQueue(q,k->right);
            }
        }
        printf("\n");
     }
}

int main(){
  int n,i,val;
  printf("請輸入節點個數:");
  scanf("%d",n);
  printf("請輸入各個節點的值:");
  Node root = NULL;
  //創建二叉查找樹
  for(i = 0; i  n; i++){
    scanf("%d",val);
    root = createBinaryTree(root,val);
  }
  //實現它的后序遍歷
  printf("遞歸實現樹的后序遍歷:");
  postOrderTraversal(root);
  printf("\n遞歸實現樹的前序遍歷:");
  preOrderTraversal(root);
  printf("\n實現樹的層序遍歷:");
  levelOrderTraversal(root);
  printf("\n遞歸實現樹的層序遍歷2\n:");
  levelOrderTraversal2(root);
  return 0;
}

運行結果:

4、二叉樹的高度

求解二叉樹某一個節點的高度的時候，我們需要獲得這個節點的左右子樹的高度，然后將兩者中的最大值加1就是當前這個節點的高度.
對應的代碼:

//節點
typedef struct NODE{
    int val;
    struct NODE *left;
    struct NODE *right;
}Node;
int getHeight(Node * root){
    int hl = 0,hr = 0,max;//hl表示的使左子樹的高度，hr表示的使右子樹的高度
    if(root != NULL){
       //當前的節點不為空，獲取左右子樹的高度
       hl = getHeight(root->left);
       hr = getHeight(root->right);
       max = hl > hr ? hl : hr;
       return max + 1;//左右子數高度的最大值加1就是當前節點的高度
    }else return 0;//如果當前節點為空，那么它的高度為0
}

5、二叉樹的刪除

二叉搜索樹的刪除需要考慮三種情況：刪除的節點是一個葉子節點、是一個含有一個子節點的節點、是一個含有兩個子節點的節點。需要綜合這三種情況進行書寫代碼。

Node deleteElement(Node root,int x){
   if(root == NULL){
     printf("節點為空，無法進行刪除操作!!!");
   }else if(x  root->val){
      root->left = deleteElement(root->left,x);
   }else if(x > root->val){
        root->right = deleteElement(root->right,x);
    }else{
      /*如果當前的節點是要刪除的節點
      判斷這個刪除的節點是否為一個葉節點，如果是，那么直接將其變成NULL即可
      否則，如果這個刪除節點只有一個子節點，那么就將子節點的值賦值給這個刪
      除節點，然后將它的子節點變成為NULL，否則，如果這個刪除節點含有兩個子節點，那么
      就將遍歷它的右子樹，獲取右子樹中的最小值，然后將這個右子樹的最小值賦值給這個
      刪除節點的值，在將這個最小值變成NULL
      */
          if(root->left != NULL  root->right != NULL){
            //刪除節點含有兩個子節點
            Node tmp = findMin(root->right);
            root->val = tmp->val;
            root->right = deleteElement(root->right,tmp->val);
          }else{
             /*
             下面的代碼如果使這樣寫的話，會發生錯誤的，為什么會這樣呢？
             其實很簡單，因為這里已經包括了兩種情況了，刪除的節點是一個葉
             節點或者只有一個子節點的節點，如果是這樣寫的話，并沒有解決刪
             除節點是一個葉節點的情況，只是把這個刪除節點的內存空間釋放了
               Node *t = root;
             if(root->left != NULL){
                root = root->left;
             }else if(root->right != NULL){
                root = root->right;
             }
             free(t);//釋放刪除的節點
             */
             Node t = root;
             if(root->left == NULL){
             /*
             如果當前節點的左子節點為空，那么就用它的右子節點替換當前節
             點，否則用左子節替換,這樣進行判斷的好處就是，如果這個刪除節點
             是一個葉節點，那么兩個子節點都是空的，那么這時候root = root-
             >right = NULL了，如果這個刪除節點含有一個子節點，并且它的左
             子節點為空，那么這個節點就用它的右子節點替換，下面的if判斷同
             理
             */
                root = root->right;
             }else if(root->right == NULL){
                root = root->left;
             }
             free(t);//釋放刪除的節點

          }
      }
   return root;
}

6、由幾種遍歷序列還原二叉樹

前序序列、中序序列還原二叉樹:

Node getBinaryTree(int preOrder_arr[],int left,int right,int inOrder_arr[],int low,int high){
  //結束遞歸的條件
  if(left >= right){
    //如果只有一個節點，那么就結束遞歸
    return NULL;
  }
  int index,root,lcount = 0,rcount = 0;
  root = preOrder_arr[left];//有前序序列得到根節點
  index = getRoot(inOrder_arr,low,high,root);//在中序數組中獲取根節點的下標
  //由根節點的下標，我們可以直到左子樹有多少個節點，右子樹有多少個節點
  lcount = index - low;
  rcount = high - index - 1;
  //創建根節點
  Node node = (Node)malloc(sizeof(struct NODE));
  node->val = root;
  //遞歸獲得根節點的左子樹
  node->left = getBinaryTree(preOrder_arr,left + 1,left + lcount + 1,inOrder_arr,low,index);
  //遞歸獲得根節點的右子樹
  node->right = getBinaryTree(preOrder_arr,left+lcount + 1,right,inOrder_arr,index + 1,high);
  return node;
}

中序序列、后序序列還原二叉樹:

//由中序序列、后序序列還原二叉樹
Node getBinaryTree2(int inOrder_arr[],int low,int high,int postOrder_arr[],int left,int right){
  if(left >= right){
    //如果只有一個節點，那么就結束遞歸
    return NULL;
  }
  int index,root,lcount = 0,rcount = 0;
  root = postOrder_arr[right - 1];//后序序列最后一個節點是根節點
  index = getRoot(inOrder_arr,low,high,root);//在中序序列中找到根節點的下標
  //創建根節點
  Node node = (Node)malloc(sizeof(struct NODE));
  node->val = root;
  //獲取左右子數的節點個數
  lcount = index - low;
  rcount = high - index - 1;
 // printf("根節點的左子樹有%d個，右子樹有%d個\n",lcount,rcount);
  //創建按根節點的左子樹
  node->left = getBinaryTree2(inOrder_arr,low,index,postOrder_arr,left,left + lcount);
  //創建根節點的右子樹
  node->right = getBinaryTree2(inOrder_arr,index + 1,high,postOrder_arr,left + lcount,right - 1);
  return node;
}

測試運行代碼:

/*
給出兩種遍歷序列（前序和中序、中序和后序），然后以這兩種序列為依據還原二叉樹
1、根據前序序列、中序序列還原二叉樹
基本思路：
   1、定義兩個數組，表示兩種序列的輸出
   2、由于前序序列，那么第一個數必定是一個根節點，所以我們有前序
   序列，在中序序列中找到根節點對應的下標，從而我們由中序序列也知道了
   根節點的左邊是他的左子樹，右邊是他的右子樹，那么我們將中序序列就劃分成為了
   兩個子數組，同時也有左、右子數的節點個數，將前序序列也劃分成為2哥子數組
   3、重復步驟2，直到子數組中的只有一個節點或者沒有，這時候結束遞歸

2、根據中序序列、后序序列還原二叉樹
基本思路:和1的一樣，只是在由后序序列找到根節點的值有所不同，因為后序序列的根節點
在最后一個，其他的步驟相似

請輸入節點的個數:12
請輸入前序序列:10 9 7 6 8 15 14 11 14 19 18 21
請輸入中序序列:6 7 8 9 10 11 14 14 15 18 19 21
請輸入后序序列:6 8 7 9 11 14 14 18 21 19 15 10
*/
#includestdio.h>
#includestdlib.h>
#define MAX_SIZE 100
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;
struct NODE{
   int val;
   Node left;
   Node right;
};
typedef struct QUEUE{
   List arr;
   int front;//隊頭指針
   int rear;//隊尾指針
}Queue;
int init(Queue s){
  s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定義一個指針類型的數組
  if(s.arr == NULL){
    return ERROR;
  }

  int i;
  //給叔組初始化之后還沒有可以，還需要給所有的節點分配空間，如果沒有這一步，那么就會發生報錯
  for(i = 0; i  MAX_SIZE; i++){
    s.arr[i] = (Node)malloc(sizeof(struct NODE));
    if(s.arr[i] == NULL)
        return ERROR;
  }
  s.front = s.rear = 0;//將隊頭指針、隊尾指針都初始為0
  return OK;
}
//壓入隊列
int pushQueue(Queue s,Node node){
   if((s.rear + 1) % MAX_SIZE == s.front){
    //如果棧滿了，返回ERROR
    printf("隊列為滿!!!\n");
    return ERROR;
   }
   s.arr[s.rear] = node;
   s.rear = (s.rear + 1) % MAX_SIZE;
   return OK;
}
int popQueue(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   s.front = (s.front + 1) % MAX_SIZE;
   return OK;
}
int getTop(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   return OK;
}
int isEmpty(Queue s){
   return s.rear == s.front;//判斷隊列是否為空
}
int getSize(Queue s){
   return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//獲取隊列的個數
}
//利用遞歸構建二叉樹
Node createBinaryTree(Node root,int x){
    if(root == NULL){
        root = (Node )malloc(sizeof(struct NODE));
        if(root == NULL){
            printf("創建節點失敗!!!\n");
            exit(0);
        }
        root->val = x;
        root->left = NULL;
        root->right = NULL;
    }else{
       //如果根節點不為空，那么就緒要找打新節點的位置
       if(x  root->val){
        //如果新節點的值比當前節點的值小，那么就需要將其往當前節點的左子樹方向找
          root->left = createBinaryTree(root->left,x);
       }else{
          root->right = createBinaryTree(root->right,x);
       }
    }
    return root;
}
//層序遍歷
void levelOrderTraversal2(Node root){
     Node t = root,k;
     Queue q;
     int size,i,count = 1;
     init(q);
     pushQueue(q,t);//將根節點壓入隊列中
     while(!isEmpty(q)){
        size = getSize(q);
        for(i = 1; i = size; i++){
            popQueue(q,k);
            printf("%5d",k->val);
            //每跳出一個節點，那么就將它的左右子節點壓入到隊列中
            if(k->left != NULL){
                pushQueue(q,k->left);
            }
            if(k->right != NULL){
                pushQueue(q,k->right);
            }
        }
        printf("\n");
     }
}
//通過循環找樹中的最小值
Node findMin(Node root){
   Node current = root;
   while(current->left != NULL){
     current = current->left;
   }
   return current;
}
//獲取二叉搜索樹的高度
int getHeight(Node root){
    int hl = 0,hr = 0,max;//hl表示的使左子樹的高度，hr表示的使右子樹的高度
    if(root != NULL){
       //當前的節點不為空，獲取左右子樹的高度
       hl = getHeight(root->left);
       hr = getHeight(root->right);
       max = hl > hr ? hl : hr;
       return max + 1;//左右子數高度的最大值加1就是當前節點的高度
    }else return 0;//如果當前節點為空，那么它的高度為0
}
/*
查找值為x的節點，然后將其返回
*/
Node findElement(Node root,int x){
   Node current = root;
   while(current != NULL){
     if(x  current->val)//如果當前的節點的值大于x的值，那么就往左子樹的方向進行查找
        current = current->left;
     else if(x > current->val)
       current = current->right;
     else
          return current;
   }
   return NULL;//如果退出循環了，說明沒有辦法找到x的節點
}
/*
刪除值為x的節點（如果x出現了多次，那么就會刪除第一個x）
這時候我們需要將分為幾種情況進行討論：
  1、刪除的節點是一個葉節點，直接將這個節點釋放即可
  2、如果刪除的節點含有一個子節點，那么這時候我們將這個刪除節點的子節點
  替換掉這個節點即可
  3、如果這個刪除節點含有兩個子節點，那么我們將它的右子樹中的最小節點的值賦給
  當前節點的值，那么這時候變成了刪除右子樹中的最小節點了（即前面的兩種情況）
*/
Node deleteElement(Node root,int x){
   if(root == NULL){
     printf("節點為空，無法進行刪除操作!!!");
   }else if(x  root->val){
      root->left = deleteElement(root->left,x);
   }else if(x > root->val){
        root->right = deleteElement(root->right,x);
    }else{
      /*如果當前的節點是要刪除的節點
      判斷這個刪除的節點是否為一個葉節點，如果是，那么直接將其變成NULL即可
      否則，如果這個刪除節點只有一個子節點，那么就將子節點的值賦值給這個刪
      除節點，然后將它的子節點變成為NULL，否則，如果這個刪除節點含有兩個子節點，那么
      就將遍歷它的右子樹，獲取右子樹中的最小值，然后將這個右子樹的最小值賦值給這個
      刪除節點的值，在將這個最小值變成NULL
      */
          if(root->left != NULL  root->right != NULL){
            //刪除節點含有兩個子節點
            Node tmp = findMin(root->right);
            root->val = tmp->val;
            root->right = deleteElement(root->right,tmp->val);
          }else{
             /*
             下面的代碼如果使這樣寫的話，會發生錯誤的，為什么會這樣呢？
             其實很簡單，因為這里已經包括了兩種情況了，刪除的節點是一個葉
             節點或者只有一個子節點的節點，如果是這樣寫的話，并沒有解決刪
             除節點是一個葉節點的情況，只是把這個刪除節點的內存空間釋放了
               Node *t = root;
             if(root->left != NULL){
                root = root->left;
             }else if(root->right != NULL){
                root = root->right;
             }
             free(t);//釋放刪除的節點
             */
             Node t = root;
             if(root->left == NULL){
             /*
             如果當前節點的左子節點為空，那么就用它的右子節點替換當前節
             點，否則用左子節替換,這樣進行判斷的好處就是，如果這個刪除節點
             是一個葉節點，那么兩個子節點都是空的，那么這時候root = root-
             >right = NULL了，如果這個刪除節點含有一個子節點，并且它的左
             子節點為空，那么這個節點就用它的右子節點替換，下面的if判斷同
             理
             */
                root = root->right;
             }else if(root->right == NULL){
                root = root->left;
             }
             free(t);//釋放刪除的節點

          }
      }
   return root;
}
//利用遞歸的方式實現后序遍歷
void postOrderDisplay(Node root){
   if(root != 0){
      postOrderDisplay(root->left);
      postOrderDisplay(root->right);
      printf("%d ",root->val);
   }
}
//利用遞歸的方式實現前序遍歷
void preOrderDisplay(Node root){
   if(root != 0){
      printf("%d ",root->val);
      preOrderDisplay(root->left);
      preOrderDisplay(root->right);
   }
}
void input(int arr[],int n){
  int i;
  for(i = 0; i  n; i++)
    scanf("%d",arr[i]);
}
int getRoot(int inOrder_arr[],int low,int high,int x){
   int i;
   for(i = low; i  high; i++){
    if(inOrder_arr[i] == x)
        return i;
   }
   return -1;
}
Node getBinaryTree(int preOrder_arr[],int left,int right,int inOrder_arr[],int low,int high){
  //結束遞歸的條件
  if(left >= right){
    //如果只有一個節點，那么就結束遞歸
    return NULL;
  }
  int index,root,lcount = 0,rcount = 0;
  root = preOrder_arr[left];//有前序序列得到根節點
  index = getRoot(inOrder_arr,low,high,root);//在中序數組中獲取根節點的下標
  //由根節點的下標，我們可以直到左子樹有多少個節點，右子樹有多少個節點
  lcount = index - low;
  rcount = high - index - 1;
  //創建根節點
  Node node = (Node)malloc(sizeof(struct NODE));
  node->val = root;
  //遞歸獲得根節點的左子樹
  node->left = getBinaryTree(preOrder_arr,left + 1,left + lcount + 1,inOrder_arr,low,index);
  //遞歸獲得根節點的右子樹
  node->right = getBinaryTree(preOrder_arr,left+lcount + 1,right,inOrder_arr,index + 1,high);
  return node;
}
//由中序序列、后序序列還原二叉樹
Node getBinaryTree2(int inOrder_arr[],int low,int high,int postOrder_arr[],int left,int right){
  if(left >= right){
    //如果只有一個節點，那么就結束遞歸
    return NULL;
  }
  int index,root,lcount = 0,rcount = 0;
  root = postOrder_arr[right - 1];//后序序列最后一個節點是根節點
  index = getRoot(inOrder_arr,low,high,root);//在中序序列中找到根節點的下標
  //創建根節點
  Node node = (Node)malloc(sizeof(struct NODE));
  node->val = root;
  //獲取左右子數的節點個數
  lcount = index - low;
  rcount = high - index - 1;
 // printf("根節點的左子樹有%d個，右子樹有%d個\n",lcount,rcount);
  //創建按根節點的左子樹
  node->left = getBinaryTree2(inOrder_arr,low,index,postOrder_arr,left,left + lcount);
  //創建根節點的右子樹
  node->right = getBinaryTree2(inOrder_arr,index + 1,high,postOrder_arr,left + lcount,right - 1);
  return node;
}
int main(){
  int preOrder_arr[MAX_SIZE],inOrder_arr[MAX_SIZE],postOrder_arr[MAX_SIZE];//定義兩個數組，分別表示前序序列、中序序列
  int n,i;
  Node root;
  printf("請輸入節點的個數:");
  scanf("%d",n);
  printf("請輸入前序序列:");
  input(preOrder_arr,n);
  printf("請輸入中序序列:");
  input(inOrder_arr,n);
  printf("請輸入后序序列:");
  input(postOrder_arr,n);
  root = getBinaryTree(preOrder_arr,0,n,inOrder_arr,0,n);
  printf("遞歸實現由前序序列、中序序列還原的二叉樹的后序遍歷:");
  postOrderDisplay(root);
  printf("\n");
  root = getBinaryTree2(inOrder_arr,0,n,postOrder_arr,0,n);
  printf("遞歸實現由中序序列、后序序列還原的二叉樹的前序遍歷:");
  preOrderDisplay(root);
  printf("\n兩種序列還原的二叉樹的高度為:");
  printf("%d\n",getHeight(root));
  printf("請輸入要刪除的節點:");
  while(scanf("%d",n) != EOF){
      if(n == 0)
        break;
      root = deleteElement(root,n);
      printf("刪除節點之后二叉樹的后序遍歷:");
      postOrderDisplay(root);
      printf("\n刪除節點之后的二叉樹的高度為:");
      printf("%d\n",getHeight(root));
      printf("刪除節點之后的層序遍歷:\n");
      levelOrderTraversal2(root);
      printf("請輸入要刪除的節點:");
  }
  return 0;
}

運行結果:

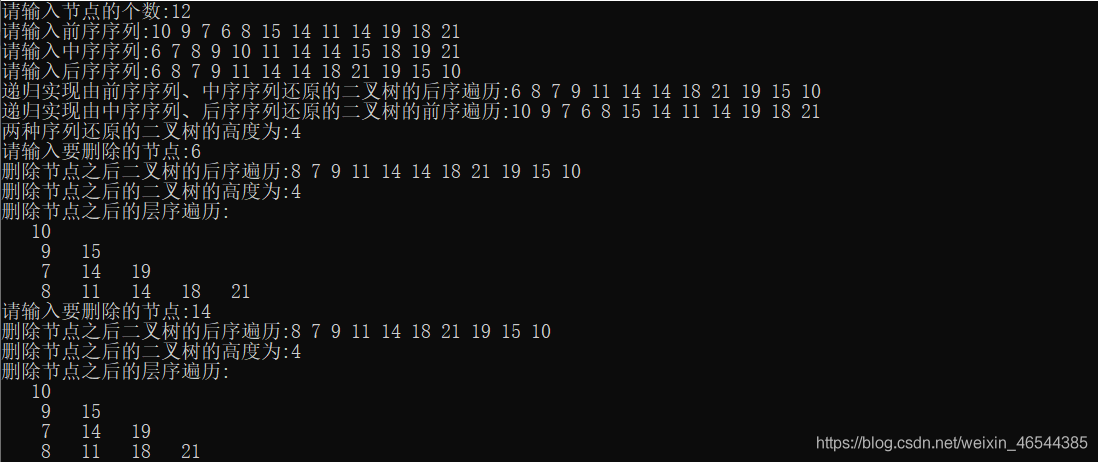
所有應用的完整代碼:

#includestdio.h>
#includestdlib.h>
#define MAX_SIZE 100
#define INCREMENT 10
#define ERROR 0
#define OK 1
typedef struct NODE * Node;
typedef Node * List;//定義二重指針
struct NODE{
   int val;
   Node left,right;
};
typedef struct QUEUE{
   List arr;
   int front;//隊頭指針
   int rear;//隊尾指針
}Queue;
int init(Queue s){
  s.arr = (List)malloc(sizeof(List) * MAX_SIZE);//定義一個指針類型的數組
  if(s.arr == NULL){
    return ERROR;
  }

  int i;
  //給叔組初始化之后還沒有可以，還需要給所有的節點分配空間，如果沒有這一步，那么就會發生報錯
  for(i = 0; i  MAX_SIZE; i++){
    s.arr[i] = (Node)malloc(sizeof(struct NODE));
    if(s.arr[i] == NULL)
        return ERROR;
  }
  s.front = s.rear = 0;//將隊頭指針、隊尾指針都初始為0
  return OK;
}
//壓入隊列
int pushQueue(Queue s,Node node){
   if((s.rear + 1) % MAX_SIZE == s.front){
    //如果棧滿了，返回ERROR
    printf("隊列為滿!!!\n");
    return ERROR;
   }
   s.arr[s.rear] = node;
   s.rear = (s.rear + 1) % MAX_SIZE;
   return OK;
}
int popQueue(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   s.front = (s.front + 1) % MAX_SIZE;
   return OK;
}
int getTop(Queue s,Node k){
   if(s.rear == s.front){
     //printf("隊列為空!!!\n");
     return ERROR;
   }
   k = s.arr[s.front];
   return OK;
}
int isEmpty(Queue s){
   return s.rear == s.front;//判斷隊列是否為空
}
int getSize(Queue s){
   return (s.rear - s.front + MAX_SIZE)%MAX_SIZE;//獲取隊列的個數
}
typedef struct STACK{
   List arr;
   int top;
}Stack;
//初始化棧
int init(Stack stack){
   stack.arr = (List)malloc(sizeof(List) * MAX_SIZE);//創建一個指針數組
   if(stack.arr == NULL){
    printf("創建節點數組失敗!!!\n");
    return ERROR;
   }
   //在創建完指針數組之后，還需要將它的節點進行分配空間，否則會發生錯誤
   int i;
   for(i = 0; i  MAX_SIZE; i++){
     stack.arr[i] = (Node)malloc(sizeof(struct NODE));
     if(stack.arr[i] == NULL){
        printf("創建節點失敗!!!\n");
        return ERROR;
     }
   }
   stack.top = 0;
   return OK;
}
//壓棧
int push(Stack stack,Node node){
   if(stack.top >= MAX_SIZE){
    //如果棧滿了，那么我們需要重新分配空間
    List newBase = (List)realloc(stack.arr,sizeof(List) * (MAX_SIZE + INCREMENT));
    if(newBase == NULL){
        printf("重新分配空間失敗!!!\n");
        return ERROR;
    }
    stack.arr = newBase;
   }
   stack.arr[stack.top++] = node;
   return OK;
}
//出棧
int pop(Stack stack,Node k){
  if(stack.top == 0)
    return ERROR;
  k = stack.arr[--stack.top];
  return OK;
}
int isEmpty(Stack stack){
  return stack.top == 0;
}
//利用遞歸創建二叉樹
Node createTree(Node T,int x){
   if(T == NULL){
     T = (Node)malloc(sizeof(struct NODE));
     if(T == NULL){
        //如果分配空間錯誤，那么輸出對應的信息，然后退出虛擬機
        printf("創建節點錯誤");
        exit(0);
     }
     T->val = x;
     T->left = NULL;
     T->right = NULL;
   }else{
      //如果當前的節點不為空，那么就需要找到x的位置
      if(x  T->val)
        T->left = createTree(T->left,x);
      else
        T->right = createTree(T->right,x);
   }
   /*
   int isLeftChild = 0;
   Node *current = T,*parent = NULL,*node = (Node *)malloc(sizeof(Node));
   while(current != NULL){
     parent = current;
     if(x  current->val){
        current = current->left;
        isLeftChild = 1;
     }else{
        current = current->right;
        isLeftChild = 0;
     }
   }
   node->val = x;
   node->left = NULL;
   node->right = NULL;
   if(parent == NULL){
      T = node;
   }else{
      if(isLeftChild){
         parent->left = node;
      }else{
         parent->right = node;
      }
   }
   */
   return T;
}
//利用非遞歸的方式進行前序遍歷(這時候需要用到棧)
void preOrderDisplay(Node t){
   Stack stack;
   init(stack);
   Node root = t,tmp;
   while(root != NULL || !isEmpty(stack)){
      while(root !=NULL){
        //將左子數的所有節點壓入到棧中
        /*
        if(root->left == NULL  root->right == NULL)
           printf("%d ",root->val);//將葉子節點輸出
           */
        printf("%d ",root->val);
        push(stack,root);
        root = root->left;
      }
      if(!isEmpty(stack)){
        //如果棧不為空，那么我們需要從棧中跳出一個節點
        pop(stack,root);
        root = root->right;
      }
   }
}
//層序遍歷
void levelOrderTraversal2(Node root){
     Node t = root,k;
     Queue q;
     int size,i,count = 1;
     init(q);
     pushQueue(q,t);//將根節點壓入隊列中
     while(!isEmpty(q)){
        size = getSize(q);
        for(i = 1; i = size; i++){
            popQueue(q,k);
            printf("%5d",k->val);
            //每跳出一個節點，那么就將它的左右子節點壓入到隊列中
            if(k->left != NULL){
                pushQueue(q,k->left);
            }
            if(k->right != NULL){
                pushQueue(q,k->right);
            }
        }
        printf("\n");
     }
}
void preOrderDisplay2(Node root){
   if(root != NULL){
   /* if(root->left == NULL  root->right == NULL)
       printf("%d ",root->val);//通過前序遍歷，將所有的葉子節點輸出
       */
    printf("%5d",root->val);
    preOrderDisplay2(root->left);
    preOrderDisplay2(root->right);
   }

}
Node findMin(Node root){
   Node current = root;
   while(current->left != NULL){
     current = current->left;
   }
   return current;
}
Node deleteElement(Node root,int x){
   if(root == NULL){
     printf("節點為空，無法進行刪除操作!!!");
   }else if(x  root->val){
      root->left = deleteElement(root->left,x);
   }else if(x > root->val){
        root->right = deleteElement(root->right,x);
    }else{
      /*如果當前的節點是要刪除的節點
      判斷這個刪除的節點是否為一個葉節點，如果是，那么直接將其變成NULL即可
      否則，如果這個刪除節點只有一個子節點，那么就將子節點的值賦值給這個刪
      除節點，然后將它的子節點變成為NULL，否則，如果這個刪除節點含有兩個子節點，那么
      就將遍歷它的右子樹，獲取右子樹中的最小值，然后將這個右子樹的最小值賦值給這個
      刪除節點的值，在將這個最小值變成NULL
      */
          if(root->left != NULL  root->right != NULL){
            //刪除節點含有兩個子節點
            Node tmp = findMin(root->right);
            root->val = tmp->val;
            root->right = deleteElement(root->right,tmp->val);
          }else{
             /*
             下面的代碼如果使這樣寫的話，會發生錯誤的，為什么會這樣呢？
             其實很簡單，因為這里已經包括了兩種情況了，刪除的節點是一個葉
             節點或者只有一個子節點的節點，如果是這樣寫的話，并沒有解決刪
             除節點是一個葉節點的情況，只是把這個刪除節點的內存空間釋放了
               Node *t = root;
             if(root->left != NULL){
                root = root->left;
             }else if(root->right != NULL){
                root = root->right;
             }
             free(t);//釋放刪除的節點
             */
             Node t = root;
             if(root->left == NULL){
             /*
             如果當前節點的左子節點為空，那么就用它的右子節點替換當前節
             點，否則用左子節替換,這樣進行判斷的好處就是，如果這個刪除節點
             是一個葉節點，那么兩個子節點都是空的，那么這時候root = root-
             >right = NULL了，如果這個刪除節點含有一個子節點，并且它的左
             子節點為空，那么這個節點就用它的右子節點替換，下面的if判斷同
             理
             */
                root = root->right;
             }else if(root->right == NULL){
                root = root->left;
             }
             free(t);//釋放刪除的節點

          }
      }
   return root;
}
/*
獲取二叉樹的高度：等于左右子樹高度的最大值加上1，那么
我們需要可以通過遞歸來獲取當前節點的左右子樹的高度，然后
將左右子樹的高度加1就是當前這個節點的高度了
*/
int getHeight(Node t){
  int hl = 0,hr = 0,max;//hl表示當前節點的左子樹的高度，hr表示的是當前節點的右子樹的高度
  if(t != NULL){
        //注意這里不是+=，而是直接賦值
    hl = getHeight(t->left);
    hr = getHeight(t->right);
    max = hl > hr ? hl : hr;
    return (max + 1);
  }else return 0;
}
int main(){
  Node root = NULL;
  int n,i,x;
  scanf("%d",n);
  for(i = 0; i  n; i++){
    scanf("%d",x);
    root = createTree(root,x);
  }
  printf("遞歸實現二叉樹的前序遍歷:");
  preOrderDisplay2(root);
  printf("\n迭代實現二叉樹的前序遍歷:");
  preOrderDisplay(root);
  printf("請輸入刪除的節點:");
  while(scanf("%d",n) != EOF){
    deleteElement(root,n);
    printf("刪除節點之后前序遍歷:");
    preOrderDisplay(root);
    printf("\n刪除節點之后層序遍歷:\n");
    levelOrderTraversal2(root);
    printf("\n二叉樹的高度為:%d\n",getHeight(root));
    printf("請輸入刪除的節點:");
  }

  return 0;
}

運行結果: